
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
【答案】
(1)
解:∵教学楼B点处观测到旗杆底端D的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,∠BAD=90°,∠ADB=30°,AB=4m,
∴AD= ![]() =
= ![]() =4
=4 ![]() (m),
(m),
答:教学楼与旗杆的水平距离是4 ![]() m.
m.
(2)
解:∵在Rt△ACD中,∠ADC=90°,∠CAD=60°,AD=4 ![]() m,
m,
∴CD=ADtan60°=4 ![]() ×
× ![]() =12(m),
=12(m),
答:旗杆CD的高度是12m.
【解析】(1)根据题意得出∠ADB=30°,进而利用锐角三角函数关系得出AD的长;
(2)利用(1)中所求,结合CD=ADtan60°求出答案.此题主要考查了解直角三角的应用,正确应用锐角三角函数关系是解题关键.


科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).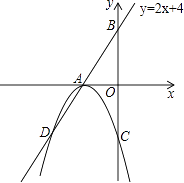
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
(1)已知灯杆垂直于路面,试标出路灯P的位置和小明在C处,头顶D在路灯投影下形成的影子N的位置.
(2)若路灯(点P)距地面8米,小明从A到C时,身影的长度是变长了还是变短了?变长或变短了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11﹣2![]() )米
)米
B.(11![]() ﹣2
﹣2![]() )米
)米
C.(11﹣2![]() )米
)米
D.(11![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是30cm幻灯片到屏幕的距离是1.5m,幻灯片上小树的高度是10cm,则屏幕上小树的高度是( )
A.50cm
B.500cm
C.60 cm
D.600cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B.∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7
B.8
C.9
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com