
如图10,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=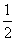 x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,
CD=4,BE=DE,△AEB的面积是2.
求证:四边形ABCD是矩形.
 |
解1:∵ AB∥CD,
∴∠EAB=∠ECD,∠EBA=∠EDC.
∵ BE=DE,
∴ △AEB≌△CED.
∴ AB=CD=4.
∵AB∥CD,
∴四边形ABCD是平行四边形.
A(2,n),B(m,n)(m>2),
∴ AB∥x轴,且CD∥x轴.
∵ m>2,∴m=6. 
∴n=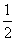 ×6+1=4.
×6+1=4.
∴ B(6,4).
∵△AEB的面积是2,
∴△AEB的高是1.
∴平行四边形ABCD的高是2.
∵ q<n,
∴q=2.
∴p=2,
即D(2,2).
∵点A(2,n),
∴DA∥y轴.
∴AD⊥CD,即∠ADC=90°.
∴四边形ABCD是矩形. 
解2:∵AB∥CD,
∴∠EAB= ∠ECD,∠EBA=∠EDC.
∠ECD,∠EBA=∠EDC.
∵ BE=DE,
∴ △AEB≌△CED.
∴ AB=CD=4.
∵AB∥CD,
∴四边形ABCD是平行四边形.
∵A(2,n),B(m,n)(m>2),
∴ AB∥x轴,且CD∥x轴.
∵ m>2,∴m=6.
∴n=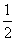 ×6+1=4.
×6+1=4.
∴ B(6,4).
过点E作EF⊥AB,垂足为F,
∵△AEB的面积是2,
∴EF=1. ∵ q<n,
∴点E的纵坐标是3.
∴点E的横坐标是4.
∴ 点F的横坐标是4.
点F的横坐标是4.
∴点F是线段AB的中点.
∴直线EF是线段AB的中垂线.
∴EA=EB.
∵四边形ABCD是平行四边形,
∴AE=EC,BE=ED.
∴AC=BD.
∴四边形ABCD是矩形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
下列说法正确的是( )
A. 掷一枚硬币,正面一定朝上
B. 某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C. 旅客上飞机前的安检应采用抽样调查
D. 方差越大,数据的波动越大
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据: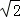 ≈1.41,
≈1.41,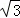 ≈1.73)
≈1.73)
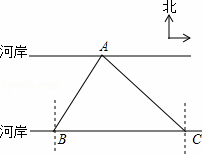
查看答案和解析>>
科目:初中数学 来源: 题型:
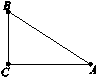
已知A,B,C三地位置如图5所示,∠C=90°,A,C两地的距离是4 km,
B,C两地的距离是3 km,则A,B两地的距离是 km;若A地在
C地的正东方向,则B地在C地的 方向.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是( )
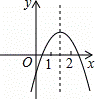
A.2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知矩形ABCD的边长分别为a,b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形In,则In的面积是 .
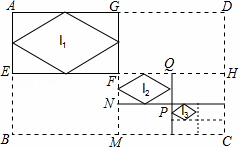
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com