
【题目】踏春时节,某班学生集体组织亲子游,沿着瓯江口樱花步道骑自行车,该班学生花了950元租了若干辆自行车,已知自行车的类型和租车价格如下表:
自行车类型 |
|
|
|
座位教(个) | 2 | 3 | 4 |
租车价格(元/辆) | 30 | 45 | 55 |
(1)若同时租用![]() 、
、![]() 两种类型的车,且共有65个座位,则应租
两种类型的车,且共有65个座位,则应租![]() 、
、![]() 类型车各多少辆?
类型车各多少辆?
(2)若![]() 型车租4辆,余下的租用
型车租4辆,余下的租用![]() 型和
型和![]() 型,要求每种车至少租用1辆,请你帮他们设计
型,要求每种车至少租用1辆,请你帮他们设计![]() 型车和
型车和![]() 型车的租车方案.
型车的租车方案.
(3)若同时租用这三类车,且每种车至少租用1辆,则最多能租到______个座位.(直接写出答案)
【答案】(1)租![]() 类型车15辆,
类型车15辆,![]() 类型车5辆(2)租A类型车11辆,
类型车5辆(2)租A类型车11辆,![]() 类型车8辆或租A类型车22辆,
类型车8辆或租A类型车22辆,![]() 类型车2辆(3)68
类型车2辆(3)68
【解析】
(1)设租![]() 类型车x辆,
类型车x辆,![]() 类型车y辆,根据题意列出二元一次方程组即可求解;
类型车y辆,根据题意列出二元一次方程组即可求解;
(2)设租A类型车a辆,![]() 类型车b辆,根据题意列出二元一次方程,求出正整数解即可求解;
类型车b辆,根据题意列出二元一次方程,求出正整数解即可求解;
(3)由表格可得A、B类车每个座位平均15元,C类车每个座位平均13.5元,故尽可能多租用C型车,再根据花费950元得到租用的车辆数.
(1)设租![]() 类型车x辆,
类型车x辆,![]() 类型车y辆,
类型车y辆,
依题意得![]()
解得![]()
答:租![]() 类型车15辆,
类型车15辆,![]() 类型车5辆;
类型车5辆;
(2)设租A类型车a辆,![]() 类型车b辆,
类型车b辆,
依题意得4×45+30a+55b=950
化简得6a+11b=154
解得正整数解为:![]() 和
和![]()
故有两种方案:租A类型车11辆,![]() 类型车8辆或租A类型车22辆,
类型车8辆或租A类型车22辆,![]() 类型车2辆;
类型车2辆;
(3)由表格可得A、B类车每个座位平均花费:30÷2=15元,C类车每个座位平均花费:55÷4=13.5元,故尽可能多租用C型车,
又950=14×55+3×30+2×45
即租用A型车3辆,B型车2辆,C型车14辆,
座位数为:3×2+2×3+14×4=68个座位
故答案为:68.


科目:初中数学 来源: 题型:
【题目】图1,是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.



(1)图2中的阴影部分的面积为 ;
(2)观察图2,三个代数式![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)若![]() ,
,![]() ,求
,求![]() ;
;
(4)观察图3,你能得到怎样的代数恒等式呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
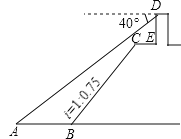
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2x3+32﹣32+5=(x+3)2﹣4,
∵(x+3)2≥0
∴当x=﹣3时,x2+6x+5有最小值﹣4.
请根据上述方法,解答下列问题:
(Ⅰ)x2+4x﹣1=x2+2x2+22﹣22﹣1=(x+a)2+b,则ab的值是_____;
(Ⅱ)求证:无论x取何值,代数式x2+2![]() x+7的值都是正数;
x+7的值都是正数;
(Ⅲ)若代数式2x2+kx+7的最小值为2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为网红城市的重庆,五一节小长假将迎来旅行的高峰,为方便外地游客的出行,重庆市某约车公司推出了一种新型的打车方式,该打车方式的费用收取是按照行驶的路程进行分段计费.小李选用了该打车方式出行,图中折线是小李打车所付车费y(元)与路程x(千米)之间的关系,请根据图象信息,解决下列问题
(1)若小李打车的路程为26千米,则小李所付的车费为 ;
(2)请求出当3≤x≤6时车费y(元)与路程x(千米)之间的关系式;
(3)若小李支付的车费为37元,求小李打车的路程.
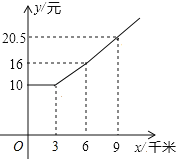
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
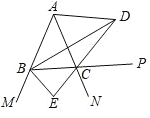
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校将举行“亲近大自然”户外活动.现随机抽取了部分学生进行主题为“你最想去的景点是”的问卷调查,要求学生只能从“A(世博园),B(劳动公园),C(月牙岛公园),D(赫图阿拉城)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图:

(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,求B(劳动公园)部分所占的圆心角度数;
(4)若该学校共有3600名学生,试估计该校最想去月牙岛公园的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com