
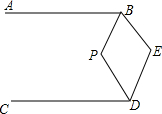
 如图,已知AB∥CD,∠E=n°,分别作∠ABE与∠CDE的角平分线交于点P,则∠P的度数为(180-$\frac{n}{2}$)°(用含n的代数式表示).
如图,已知AB∥CD,∠E=n°,分别作∠ABE与∠CDE的角平分线交于点P,则∠P的度数为(180-$\frac{n}{2}$)°(用含n的代数式表示). 分析 过点E作EF∥AB,由EF∥AB∥CD可得∠ABE+∠BEF=180°、∠∠CDE+∠DEF=180°,结合∠BEF+∠DEF=∠E=n°以及四边形BEFP内角和为360°即可得出∠P的度数.
解答 解:过点E作EF∥AB,如图所示.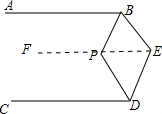
∵EF∥AB,
∴∠ABE+∠BEF=180°,
∵EF∥AB∥CD,
∴∠CDE+∠DEF=180°.
∴∠ABE+∠BEF+∠DEF+∠CDE=360°,
又∵∠BEF+∠DEF=∠E=n°,
∴∠ABE+∠CDE=(360-n)°.
∵分别作∠ABE与∠CDE的角平分线交于点P,
∴∠PBE+∠PDE=$\frac{1}{2}$(∠ABE+∠CDE)=180°-$\frac{n°}{2}$,
∵∠P+∠E+∠PBE+∠PDE=360°,
∴∠P=(180-$\frac{n}{2}$)°.
故答案为:(180-$\frac{n}{2}$).
点评 本题考查了平行线的性质、角的运算以及四边形的内角和,解题的关键是通过平行找出角的关系.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
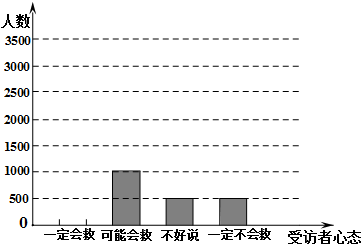 2011年10月13日下午5时30分,在广东佛山南海黄岐镇广佛五金城,两岁的“悦悦”被迎面驶来的面包车撞倒卷到车底.因无人施救,“悦悦”被小型货柜车再次碾压.之后往来的十余个路人均见死不救,直到一位拾荒阿姨看到并救起“悦悦”.“小悦悦事件”发生后,立刻引起全社会的关注与反思.某社会调查中心通过网络,发起“拒绝冷漠,关爱他人”的调查活动,对部分网民进行在线调查.下面是根据调查结果绘制的受访者年龄频数分布表和受访者心态分布直方图(单位:人).读图、表,回答下列问题:(“60后”是指出生在上世纪60年代的人,以下类推)
2011年10月13日下午5时30分,在广东佛山南海黄岐镇广佛五金城,两岁的“悦悦”被迎面驶来的面包车撞倒卷到车底.因无人施救,“悦悦”被小型货柜车再次碾压.之后往来的十余个路人均见死不救,直到一位拾荒阿姨看到并救起“悦悦”.“小悦悦事件”发生后,立刻引起全社会的关注与反思.某社会调查中心通过网络,发起“拒绝冷漠,关爱他人”的调查活动,对部分网民进行在线调查.下面是根据调查结果绘制的受访者年龄频数分布表和受访者心态分布直方图(单位:人).读图、表,回答下列问题:(“60后”是指出生在上世纪60年代的人,以下类推) | 分 组 | 频 数 | 频 率 |
| “60后”网民 | 300 | 0.06 |
| “70后”网民 | 500 | a |
| “80后”网民 | b | 0.30 |
| “90后”网民 | 2600 | c |
| 其 它 | 100 | 0.02 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{k}{x}$(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,那么图中阴影部分的面积之和为$\frac{49}{18}$,则k的值为4.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{k}{x}$(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,那么图中阴影部分的面积之和为$\frac{49}{18}$,则k的值为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com