
【题目】如图,在△ABC中,AB=AC,点D是BC边的中点,连接AD,分别过点A,C作AE∥BC,CE∥AD交于点E,连接DE,交AC于点O.
(1)求证:四边形ADCE是矩形;
(2)若AB=10,sin∠COE=![]() ,求CE的长.
,求CE的长.
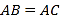
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() 的平分线
的平分线![]() 与
与![]() 轴相较于点
轴相较于点![]() ,
,![]() 、
、![]() 两点关于
两点关于![]() 轴对称.
轴对称.
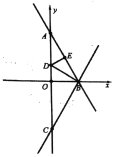
(1)一动点![]() 从点
从点![]() 出发,沿适当的路径运动到直线
出发,沿适当的路径运动到直线![]() 上的点
上的点![]() ,再沿适当的路径运动到点
,再沿适当的路径运动到点![]() 处.当
处.当![]() 的运动路径最短时,求此时点
的运动路径最短时,求此时点![]() 的坐标及点
的坐标及点![]() 所走最短路径的长.
所走最短路径的长.
(2)点![]() 沿直线
沿直线![]() 水平向右运动得点
水平向右运动得点![]() ,平面内是否存在点
,平面内是否存在点![]() 使得以
使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,请直接写出点
为顶点的四边形为菱形,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
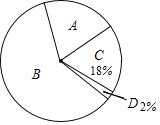
【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
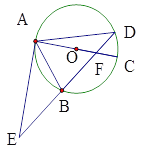
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.
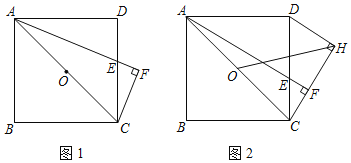
(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;
(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;
(3)当E为DC中点时,AC=2![]() ,直接写出AF的长 .
,直接写出AF的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a、b、c,用Ma,b,c表示这三个数的中位数,用maxa,b,c表示这三个数中最大数,例如:M2,1,01,max2,1,00,max2,1,a![]() 解决问题:Msin45,cos60,tan60_____,如果max3,53x,2x63,则x的取值范围为______.
解决问题:Msin45,cos60,tan60_____,如果max3,53x,2x63,则x的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
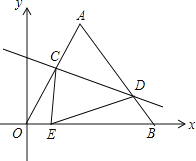
【题目】如图坐标系中,O(0,0),A(3,3![]() ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中数学 来源: 题型:
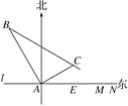
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com