
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为![]() (单位:km),乘坐地铁的时间
(单位:km),乘坐地铁的时间![]() (单位:min)是关于
(单位:min)是关于![]() 的一次函数,其关系如下表:
的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x/km | 7 | 9 | 11 | 12 | 13 |
y1/min | 16 | 20 | 24 | 26 | 28 |
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)李华骑单车的时间![]() (单位:min)也受
(单位:min)也受![]() 的影响,其关系可以用
的影响,其关系可以用![]() =
=![]()
![]() 2-11
2-11![]() +78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
+78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
【答案】(1) y1=2x+2 ;(2) 李华应选择在B站出地铁,才能使他从文化宫站回到家所需的时间最短,最短时间为39.5 min
【解析】
(1)将(7,16),(9,20)代入一次函数解析式,便可求解.
(2)回到家所需的时间为y,则y=y1+y2,y= =![]() x2-9x+80配方便可解决.
x2-9x+80配方便可解决.
解:(1)设y1关于x的函数解析式为y1=kx+b.将(7,16),(9,20)代入,
得![]() 解得
解得![]() ∴y1关于x的函数解析式为y1=2x+2.
∴y1关于x的函数解析式为y1=2x+2.
(2)设李华从文化宫站回到家所需的时间为y min,y=y1+y2
则y=y1+y2=2x+2+![]() x2-11x+78=
x2-11x+78=![]() x2-9x+80=
x2-9x+80=![]() (x-9)2+39.5.
(x-9)2+39.5.
∴当x=9时,y取得最小值,最小值为39.5.
所以李华应选择在B站出地铁,才能使他从文化宫站回到家所需的时间最短,最短时间为39.5 min.


科目:初中数学 来源: 题型:
【题目】某同学进行社会调查,随机抽查了某个小区的200户家庭的年收入,并绘制成统计图(如图).请你根据统计图给出的信息回答:
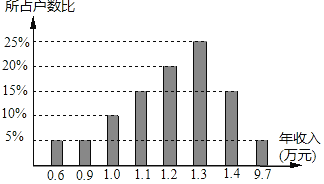
(1)样本数据的中位数是_____,众数是_____;
(2)这200户家庭的平均年收入为_____万元;
(3)在平均数、中位数两数中,_____更能反映这个小区家庭的年收入水平.
(4)如果该小区有1200户住户,请你根据抽样调查的结果估计该小区有_____户家庭的年收入低于1.3万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为且在
为且在![]() 的右侧作正方形
的右侧作正方形![]() .
.

(1)如果![]() ,当点
,当点![]() 在线段BC上时(与点
在线段BC上时(与点![]() 不重合),①如图2,线段
不重合),①如图2,线段![]() 的数量关系为 ,线段
的数量关系为 ,线段![]() 所在直线的位置关系为 ;
所在直线的位置关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如,3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如,3,①中的结论是否仍然成立,并说明理由;
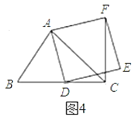
(2)如图4,如果![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),请直接写出答案.
不重合),请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为1的正方形![]() 的两个顶点
的两个顶点![]() ,
,![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是原点.现在将正方形
是原点.现在将正方形![]() 绕原点
绕原点![]() 顺时针旋转,当点
顺时针旋转,当点![]() 第一次落在直线
第一次落在直线![]() 上时停止.旋转过程中,
上时停止.旋转过程中,![]() 边交直线
边交直线![]() 于点
于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
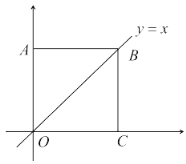
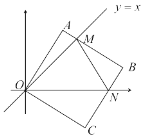
(1)若点![]() ,求此时点
,求此时点![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)若![]() 的周长是
的周长是![]() ,在旋转过程中,
,在旋转过程中,![]() 值是否会发生变化?若不变,请求出这个定值,若有变化,请说明理由;
值是否会发生变化?若不变,请求出这个定值,若有变化,请说明理由;
(3)设![]() ,当
,当![]() 为何值时
为何值时![]() 的面积最小,最小值是多少?并直接写出此时
的面积最小,最小值是多少?并直接写出此时![]() 内切圆半径.
内切圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
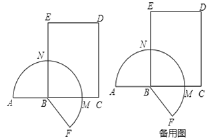
【题目】如图,点![]() 为长为5的线段
为长为5的线段![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,且
,且![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,将线段
,将线段![]() 绕点B顺时针旋转,得到线段
绕点B顺时针旋转,得到线段![]() ,优弧
,优弧![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,设旋转角为
,设旋转角为![]()
(1)若扇形![]() 的面积为
的面积为![]() ,则
,则![]() 的度数为_______.
的度数为_______.
(2)连接![]() ,判断
,判断![]() 与扇形
与扇形![]() 所在圆
所在圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设![]() 为直线
为直线![]() 上一点,沿
上一点,沿![]() 所在直线折叠矩形,若折叠
所在直线折叠矩形,若折叠![]() 后所在的直线与扇形
后所在的直线与扇形![]() 所在
所在![]() 的相切,求
的相切,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
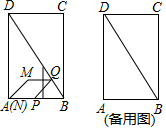
【题目】如图,在矩形ABCD中,AB=2cm,∠ADB=30°.P,Q两点分别从A,B同时出发,点P沿折线AB﹣BC运动,在AB上的速度是2cm/s,在BC上的速度是2![]() cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
(1)当PQ⊥AB时,x等于多少;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)直线AM将矩形ABCD的面积分成1:3两部分时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学可以让人高雅,益智,豪情逸致,某中学为开拓学生视野,开展“课外学数学”活动,随机调查了九年级部分学生一周的课外学习数学时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
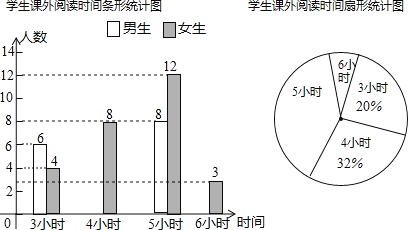
(1)本次调查的学生总数为____________人,被调查学生课外学习数学时间的中位数是____________小时,众数是 小时;
(2)请你补全条形统计图;
(3)在扇形统计图中,课外学习数学时间为5小时的扇形的圆心角度数是____________;
(4)九年级有学生700人,估计九年级一周课外学习数学时间不少于5小时小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
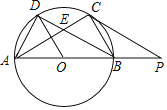
【题目】如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)求证:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的长;
(3)在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com