练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    一条公路上有n个工厂，现在要在公路边建一个货物中转站P，使得这n个工厂到货物中转站的距离之和最小，应建在哪？
    考点：直线、射线、线段
    专题：
    分析：分两种情况①当n是奇数、选最中间的一个工厂作为货物中转站P，②n是偶数，中间两个点工厂之间任何地方都可以建一个货物中转站P．
    解答：解：找到让两边的工厂同样多的那个点．
    ①当n是奇数、选最中间的一个工厂作为货物中转站P，可得这n个工厂到货物中转站的距离之和最小，
    ②n是偶数，中间两个点工厂之间任何地方都可以建一个货物中转站P，使得这n个工厂到货物中转站的距离之和最小，
    点评：本题主要考查了直线、射线、线段，解题的关键是分两种情况讨论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知△ABC中，AB=AC，CD⊥AB于点D．
    （1）若∠A=36°，求∠DCB的度数；
    （2）若AB=10，CD=6，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）
    a-a2
    a-1
    -1+a
    （2）（3
    		12
    -2
    1
    3
    +
    		48
    ）÷2
    		3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一辆自行车轮胎的外直径约是72cm，如果平均每分钟转100周，它通过一座452.16m长的大桥，需要多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下午2点24分，时钟的时针和分针的夹角是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知∠AOB=60°，作射线OC，使∠AOC=28°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知|x-1|+（2y+1）2+（4z+2）2=0，则2x-y+z=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

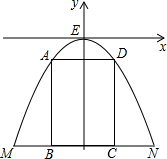    如图，某公路隧道横截面为抛物线，其最高点E距离路面4米，底部宽度MN为4米，因维修要搭建一个高度为3米的矩形形状的“支撑架”，已知矩形ABCD的两个顶点A、D在抛物线上，B、C两点在地面MN上，求所需的矩形“支撑架”的周长，为解决这个问题，小明想出了一个方法：以E为坐标原点，MN的中垂线为y轴，建立平面直角坐标系，先求出抛物线的解析式，再解决．请你替小明求出抛物线的解析式，再求出这个“支撑架”的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

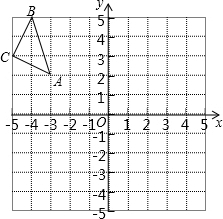    如图，在平面直角坐标系中，每个小正方形的边长为1，点A的坐标为（-3，2）．
    （1）利用关于坐标轴对称的点的坐标的特点画出△ABC关于x轴的对称图形△A1B1C1和△ABC关于y轴的对称图△A2B2C2．
    （2）写出点A1和点C2的坐标．

    查看答案和解析>>

    同步练习册答案