
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ,
,![]() ЃЌвдOBЮЊБпЃЌдк
ЃЌвдOBЮЊБпЃЌдк![]() ЭтзїЕШБп
ЭтзїЕШБп![]() ЃЌDЪЧOBЕФжаЕуЃЌСЌНгADВЂбгГЄНЛOCгкEЃЎ
ЃЌDЪЧOBЕФжаЕуЃЌСЌНгADВЂбгГЄНЛOCгкEЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCEЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉСЌНгACЃЌBEНЛгкЕуPЃЌЧѓAPЕФГЄМАAPБпЩЯЕФИпBHЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЫФБпаЮOABCжУгкШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕжаЃЌвдEЮЊзјБъдЕуЃЌЦфгрЬѕМўВЛБфЃЌвдAPЮЊБпЯђгвЩЯЗНзїе§ЗНаЮAPMNЃК
ЂйMЕуЕФзјБъЮЊ ЃЎ
ЂкжБНгаДГіе§ЗНаЮAPMNгыЫФБпаЮOABCжиЕўВПЗжЕФУцЛ§ЃЈЭМжавѕгАВПЗжЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУжБНЧШ§НЧаЮаББпжаЯпЕФаджЪПЩЕУDO=DAЃЌЭЦГіЁЯAEO=60ЁуЃЌНјвЛВНЕУГіBCЁЮAEЃЌCOЁЮABЃЌПЩЕУНсТлЃЛ
ЃЈ2ЃЉЯШМЦЫуГіOA=![]() ЃЌЭЦГіPB=
ЃЌЭЦГіPB=![]() ЃЌРћгУЙДЙЩЖЈРэЧѓГіAP=
ЃЌРћгУЙДЙЩЖЈРэЧѓГіAP=![]() ЃЌдйРћгУУцЛ§ЗЈМЦЫуBHМДПЩЃЛ
ЃЌдйРћгУУцЛ§ЗЈМЦЫуBHМДПЩЃЛ
ЃЈ3ЃЉЂйЧѓГіжБЯпPMЕФНтЮіЪНЮЊy=![]() x-3ЃЌдйРћгУСНЕуМфЕФОрРыЙЋЪНМЦЫуМДПЩЃЛ
x-3ЃЌдйРћгУСНЕуМфЕФОрРыЙЋЪНМЦЫуМДПЩЃЛ
ЂквзЕУжБЯпBCЕФНтЮіЪНЮЊy=![]() x+4ЃЌСЊСЂжБЯпBCКЭжБЯпPMЕФНтЮіЪНГЩЗНГЬзщЃЌЧѓЕУЕуGЕФзјБъЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНМЦЫуЃЎ
x+4ЃЌСЊСЂжБЯпBCКЭжБЯпPMЕФНтЮіЪНГЩЗНГЬзщЃЌЧѓЕУЕуGЕФзјБъЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНМЦЫуЃЎ
ЃЈ1ЃЉжЄУїЃКЁпRtЁїOABжаЃЌDЮЊOBЕФжаЕуЃЌ
ЁрAD=![]() OBЃЌOD=BD=
OBЃЌOD=BD=![]() OBЃЌ
OBЃЌ
ЁрDO=DAЃЌ
ЁрЁЯDAO=ЁЯDOA=30ЁуЃЌЁЯEOA=90ЁуЃЌ
ЁрЁЯAEO=60ЁуЃЌ
гжЁпЁїOBCЮЊЕШБпШ§НЧаЮЃЌ
ЁрЁЯBCO=ЁЯAEO=60ЁуЃЌ
ЁрBCЁЮAEЃЌ
ЁпЁЯBAO=ЁЯCOA=90ЁуЃЌ
ЁрCOЁЮABЃЌ
ЁрЫФБпаЮABCEЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉНтЃКдкRtЁїAOBжаЃЌЁЯAOB=30ЁуЃЌOB=8ЃЌ
ЁрAB=4ЃЌ
ЁрOA=![]() ЃЌ
ЃЌ
ЁпЫФБпаЮABCEЪЧЦНааЫФБпаЮЃЌ
ЁрPB=PEЃЌPC=PAЃЌ
ЁрPB=![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
МД![]()
Ёр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйЁпCЃЈ0ЃЌ4ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=kx+4ЃЌ
ЁпPЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
Ёр0=![]() k+4ЃЌ
k+4ЃЌ
НтЕУЃЌk=![]() ЃЌ
ЃЌ
Ёрy=![]() x+4ЃЌ
x+4ЃЌ
ЁпЁЯAPM=90ЁуЃЌ
ЁржБЯпPMЕФНтЮіЪНЮЊy=![]() x+mЃЌ
x+mЃЌ
ЁпPЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
Ёр0=![]() ЁС
ЁС![]() +mЃЌ
+mЃЌ
НтЕУЃЌm=-3ЃЌ
ЁржБЯпPMЕФНтЮіЪНЮЊy=![]() x-3ЃЌ
x-3ЃЌ
ЩшMЃЈxЃЌ![]() x-3ЃЉЃЌ
x-3ЃЉЃЌ
ЁпAP=![]() ЃЌ
ЃЌ
ЁрЃЈx-![]() ЃЉ2+ЃЈ
ЃЉ2+ЃЈ![]() x-3ЃЉ2=ЃЈ
x-3ЃЉ2=ЃЈ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЛЏМђЕУЃЌx2-4![]() x-4=0ЃЌ
x-4=0ЃЌ
НтЕУЃЌx1=![]() ЃЌx2=
ЃЌx2=![]() ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЕБx=![]() ЪБЃЌy=
ЪБЃЌy=![]() ЁСЃЈ
ЁСЃЈ![]() ЃЉ-3=
ЃЉ-3=![]() ЃЌ
ЃЌ
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЁп![]()
ЁржБЯпBCЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
СЊСЂ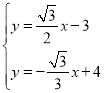 ЃЌНтЕУ
ЃЌНтЕУ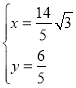 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪжЛњОЯњЩЬМЦЛЎЙКНјЦЛЙћЪжЛњЕФ iPhone8ЁЂ iphone8PlusЁЂ iphoneXШ§ПюЪжЛњЙВ60ВПЃЌУППюЪжЛњжСЩйвЊЙКНј10ВПЃЌЧвЧЁКУгУЭъЙКЛњПю360000дЊЃЎЩшЙКНјiPhone8ЪжЛњ![]() ВПЃЌiPhone8PlusЪжЛњ
ВПЃЌiPhone8PlusЪжЛњ![]() ВПЃЎШ§ПюЪжЛњЕФНјМлКЭЪлМлШчБэЃК
ВПЃЎШ§ПюЪжЛњЕФНјМлКЭЪлМлШчБэЃК
ЪжЛњаЭКХ | iPhone8 | iphone8Plus | iphoneX |
НјМлЃЈдЊВПЃЉ | 4600 | 6100 | 7600 |
ЪлМлЃЈдЊВПЃЉ | 5200 | 6800 | 8600 |
ЃЈ1ЃЉгУКЌ![]() ЃЌ
ЃЌ![]() ЕФЪНзгБэЪОЙКНјiphoneXЪжЛњЕФВПЪ§ЃЎ
ЕФЪНзгБэЪОЙКНјiphoneXЪжЛњЕФВПЪ§ЃЎ
ЃЈ2ЃЉЧѓГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉМйЩшЫљЙКНјЪжЛњШЋВПЪлГіЃЎ
ЂйЧѓГідЄЙРРћШѓ![]() ЃЈдЊЃЉгы
ЃЈдЊЃЉгы![]() ЃЈВПЃЉЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈВПЃЉЕФКЏЪ§ЙиЯЕЪНЃЎ
ЂкЧѓГідЄЙРРћШѓЕФзюДѓжЕЃЌВЂаДГіДЫЪБЙКНјШ§ПюЪжЛњИїЖрЩйВПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШдФЖСЃЌдйЬюПеНтД№ЃК
ЗНГЬ![]() ЕФИљЮЊ
ЕФИљЮЊ![]() ЃЛ
ЃЛ
ЗНГЬ![]() ЕФИљЮЊ
ЕФИљЮЊ![]() .
.
ЂХЃЎЗНГЬ![]() ЕФИљЪЧ
ЕФИљЪЧ![]()
![]()
ЂЦЃЎШє![]() ЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬ
ЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬ![]() ЕФСНИіЪЕЪ§ИљЃЌФЧУД
ЕФСНИіЪЕЪ§ИљЃЌФЧУД![]() гыЯЕЪ§aЁЂbЁЂcЕФЙиЯЕЪЧЃК
гыЯЕЪ§aЁЂbЁЂcЕФЙиЯЕЪЧЃК![]()
ЂЧЃЎШчЙћ![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФСНИіИљЃЌИљОнЂЦЫљЕУЕФНсТлЃЌЧѓ
ЕФСНИіИљЃЌИљОнЂЦЫљЕУЕФНсТлЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВМДќРягаЫФИіаЁЧђЃЌЧђБэУцЗжБ№Бъга2ЁЂ3ЁЂ4ЁЂ6ЫФИіЪ§зжЃЌЫќУЧЕФВФжЪЁЂаЮзДЁЂДѓаЁЭъШЋЯрЭЌЁЃДгжаЫцЛњУўГівЛИіаЁЧђМЧЯТЪ§зжЮЊxЃЌдйДгЪЃЯТЕФШ§ИіЧђжаЫцЛњУўГівЛИіЧђМЧЯТЪ§зжЮЊyЃЌЕуAЕФзјБъЮЊЃЈx,y).дЫгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌаДГіAЕуЫљгаПЩФмЕФзјБъЃЌВЂЧѓГіЕуAдкЗДБШР§КЏЪ§![]() ЭМЯѓЩЯЕФИХТЪ.
ЭМЯѓЩЯЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDНЛABгкЕуPЃЌAPЃН2ЃЌBPЃН6ЃЌЁЯAPCЃН30ЁуЃЌдђCDЕФГЄЮЊ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§ЕФЭМЯѓгыxжсНЛгкAЃЈЉ2ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌЧвКЏЪ§ОЙ§ЕуЃЈ3ЃЌ10ЃЉЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшетИіЖўДЮКЏЪ§ЕФЖЅЕуЮЊPЃЌЧѓЁїABPЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕБxЮЊКЮжЕЪБЃЌyЁм0ЃЎЃЈЧыжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
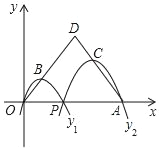
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїAODЪЧЕШбќШ§НЧаЮЃЌЕуAЃЈ12ЃЌ0ЃЉЃЌOЮЊзјБъдЕуЃЌPЪЧЯпЖЮOAЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕуOЃЌAЃЉЃЌЙ§PЃЌOСНЕуЕФЖўДЮКЏЪ§y1ЃЌКЭЙ§PЁЂAСНЕуЕФЖўДЮКЏЪ§y2ЃЌЕФПЊПкОљЯђЯТЃЌЫќУЧЕФЖЅЕуЗжБ№ЮЊBЃЌCЃЌЕуBЃЌCЗжБ№дкODЁЂADЩЯЃЎЕБOD=AD=10ЪБЃЌдђСНИіЖўДЮКЏЪ§ЕФзюДѓжЕжЎКЭЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=4ЃЌBC=3ЃЌOЪЧЁїABCЕФФкаФЃЌвдOЮЊдВаФЃЌrЮЊАыОЖЕФдВгыЯпЖЮABгаНЛЕуЃЌдђrЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
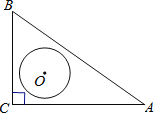
AЃЎrЁн1 BЃЎ1ЁмrЁм![]() CЃЎ1ЁмrЁм
CЃЎ1ЁмrЁм![]() DЃЎ1ЁмrЁм4
DЃЎ1ЁмrЁм4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЩњВњAжжВњЦЗЃЌЫќЕФГЩБОЪЧ6дЊ/МўЃЌЪлМлЪЧ8дЊ/МўЃЌФъЯњЪлСПЮЊ5ЭђМўЃЎЮЊСЫЛёЕУИќКУЕФаЇвцЃЌЙЋЫОзМБИФУГівЛЖЈЕФзЪН№зіЙуИцЃЌИљОнОбщЃЌУПФъЭЖШыЕФЙуИцЗбЪЧxЭђдЊЃЌВњЦЗЕФФъЯњЪлСПНЋЪЧдЯњЪлСПЕФyБЖЃЌЧвyгыxжЎМфТњзуЮвУЧбЇЙ§ЕФЖўжжКЏЪ§ЃЈМДвЛДЮКЏЪ§КЭЖўДЮКЏЪ§ЃЉЙиЯЕжаЕФвЛжжЃЌЫќУЧЕФЙиЯЕШчЯТБэЃК
xЃЈЭђдЊЃЉ | 0 | 0.5 | 1 | 1.5 | 2 | Ё |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | Ё |
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉ
ЃЈ2ЃЉШчЙћАбРћШѓПДзїЪЧЯњЪлзмЖюМѕШЅГЩБОЗбгУКЭЙуИцЗбгУЃЌЪдЧѓГіФъРћШѓWЃЈЭђдЊЃЉгыЙуИцЗбгУxЃЈЭђдЊЃЉЕФКЏЪ§ЙиЯЕЪНЃЌВЂМЦЫуУПФъЭЖШыЕФЙуИцЗбЪЧЖрЩйЭђдЊЪБЫљЛёЕУЕФРћШѓзюДѓЃП
ЃЈ3ЃЉШчЙћЙЋЫОЯЃЭћФъРћШѓWЃЈЭђдЊЃЉВЛЕЭгк14ЭђдЊЃЌЧыФуАяЙЋЫОШЗЖЈЙуИцЗбЕФЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com