
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(5)方程去括号,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:10x-15-6-12x=3,
移项合并得:-2x=24,
解得:x=-12;
(2)去分母得:3x-3-4x-6=6,
移项合并得:-x=15,
解得:x=-15;
(3)去分母得:6-x+1=6x-2,
移项合并得:7x=9,
解得:x=$\frac{9}{7}$;
(4)去分母得:10x+2-2x+1=6,
移项合并得:8x=3,
解得:x=$\frac{3}{8}$;
(5)去括号得:12x+4-8=2x-5,
移项合并得:10x=-1,
解得:x=-$\frac{1}{10}$;
(6)去分母得:9-21x=5-20x-15,
移项合并得:x=19.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
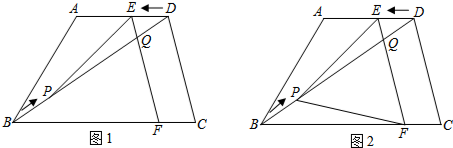
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:| A. | ①②③④ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)
苹果熟了,一个苹果从树上被抛下.如图所示,从A处落到了B处.(网格单位长度为1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{11}{36}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com