Question

11．如图，在梯形ABCD中，AD∥BC，AD=6cm，CD=8cm，BC=BD=10cm，点P由B出发沿BD方向匀速运动，速度为
1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为1cm/s，交BD于Q，连接PE．若设运动时间为t（s）（0＜t＜5）．解答下列问题：
（1）当t为何值时，PE∥AB？
（2）是否存在某一时刻t，使S_△DEQ=$\frac{1}{25}{S}_{△BCD}$？若存在，求出此时t的值；若不存在，说明理由．
（3）如图2连接PF，在上述运动过程中，五边形PFCDE的面积是否发生变化？说明理由．

Answer 1

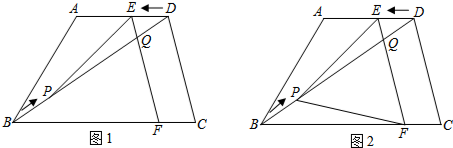
分析 （1）若要PE∥AB，则应有$\frac{DE}{DA}=\frac{DP}{DB}$，故用t表示DE和DP后，代入上式求得t的值；
（3）利用S_△DEQ=$\frac{1}{25}{S}_{△BCD}$建立方程，求得t的值；
（4）易得△PDE≌△FBP，故有S_{五边形PFCDE}=S_△PDE+S_{四边形PFCD=}S_△FBP+S_{四边形PFCD}=S_△BCD，即五边形的面积不变．

解答 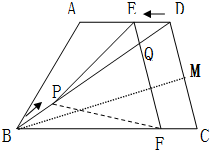解：（1）据题意得DE=BP=t，则DP=10-t，
∵PE∥AB，
∴$\frac{DE}{DA}=\frac{DP}{DB}$，
∴$\frac{t}{6}=\frac{10-t}{10}$，
∴t=$\frac{15}{4}$，
∴当t=$\frac{15}{4}$（s）时，PE∥AB；

（2）存在，
∵DE∥BC，
∴△DEQ∽△BCD，
∴$\frac{{S}_{△EDQ}}{{S}_{△BCD}}$=（$\frac{DE}{BC}$）²，
∵S_△DEQ=$\frac{1}{25}{S}_{△BCD}$，
∴$\frac{{S}_{△EDQ}}{{S}_{△BCD}}$=（$\frac{DE}{BC}$）²=$\frac{1}{25}$，
∴（$\frac{t}{10}$）²=$\frac{1}{25}$，
∴t²=$\frac{1}{25}$×100=4；
t₁=2，t₂=-2（不合题意舍去），
∴当t=2时，S_△DEQ=$\frac{1}{25}{S}_{△BCD}$；

（3）不变．过B作BM⊥CD，交CD于M
∴S_△BCD=$\frac{1}{2}CD•$BM=$\frac{1}{2}×8×2\sqrt{21}$=8$\sqrt{21}$，
在△PDE和△FBP中，$\left\{\begin{array}{l}{DE=BP=t}\\{∠PDE=∠FBP}\\{PD=BF=10-t}\\{\;}\end{array}\right.$，
∴△PDE≌△FBP，
∴S_{五边形PFCDE}=S_△PDE+S_{四边形PFCD=}S_△FBP+S_{四边形PFCD}=S_△BCD=8$\sqrt{21}$，
∴在运动过程中，五边形PFCDE的面积不变．

点评 本题利用了平行线的性质，相似三角形和全等三角形的判定和性质，勾股定理，三角形的面积公式求解．综合性较强，难度较大．