
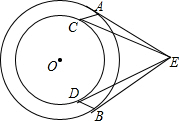
 已知两个同心圆,EA、EB是大圆的两条切线,EC、ED是小圆的两条切线,A、B、C、D为切点.求证:AC=BD.
已知两个同心圆,EA、EB是大圆的两条切线,EC、ED是小圆的两条切线,A、B、C、D为切点.求证:AC=BD. 分析 连接OP,根据切线长定理得出AE=BE,CE=DE,∠AEO=∠BEO,∠CEO=∠DEO,进而得出∠AEC=∠BED,然后根据SAS证得△AEC≌△BED,根据全等三角形的性质即可证得结论.
解答 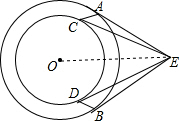 证明:连接OP,
证明:连接OP,
∵两个同心圆,EA、EB是大圆的两条切线,EC、ED是小圆的两条切线,
∴AE=BE,CE=DE,∠AEO=∠BEO,∠CEO=∠DEO,
∴∠AEO-∠CEO=∠BEO-∠DEO,即∠AEC=∠BED,
在△AEC和△BED中
$\left\{\begin{array}{l}{AE=BE}\\{∠AEC=∠BED}\\{CE=DE}\end{array}\right.$
∴△AEC≌△BED(SAS),
∴AC=BD.
点评 本题考查了切线的性质,切线长定理的应用,三角形全等的判定和性质,熟练掌握性质定理是解题的关键.


科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=20°,则∠1的度数为 度.
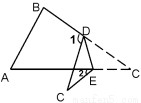
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:判断题
在圣诞节前夕,几位同学到某文具店调查一种进价为2元的圣诞贺卡的销售情况,每张定价3元,每天能卖出500张,每张售价每上涨0.1元,其每天销售量就减少10个.另外,物价局规定,售价不得超过商品进价的240%.据此,请你解答下面问题:
(1)要实现每天800元的利润,应如何定价?
(2)800元的利润是否最大?如何定价,才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
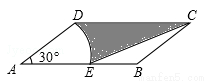
如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )
ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )
A. 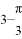 B.
B. 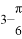 C.
C. 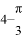 D.
D. 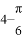
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
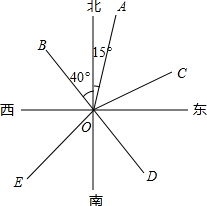 如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一只渔船从岛A出发沿北偏东30°方向航行了50海里,遇到岛瞧(B点),又沿西北方向航行了25海里(此时记为C点).
如图,一只渔船从岛A出发沿北偏东30°方向航行了50海里,遇到岛瞧(B点),又沿西北方向航行了25海里(此时记为C点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com