
【题目】正方形ABCD中,点P为直线BC上的一点,DP的垂直平分线交射线DC于M,交DP于E,交射线AB于N.
(1)当点M在CD边上时如图①,易证PM-CP=AN;
(2)当点M在CD边延长线上如图②、图③的位置时,上述结论是否成立?写出你的猜想,并对图②给予证明.



图① 图② 图③
【答案】图②:PM+CP=AN;图③:PM-CP=AN,证明见解析.
【解析】(1)过N作NQ∥AD,则NQ=AD,AN=DQ,易证∠MNQ=∠PDC,即可证明△MNQ≌△PDC,可得QM=PC,再根据垂直平分线性质可得DM=PM,即可解题;
(2)①作MQ∥BF,则AQ=DM,QM=AD=CD,易证∠NMQ=∠MDE,即可证明△NMQ≌△PDC,可得QN=PC,再根据垂直平分线性质可得PM=AQ,即可解题;
③作NQ∥BC,则NQ=AD=CD,AN=DQ,易证∠NMD=∠CPD,即可证明△CDP≌△EDM,可得QM=CP,再根据垂直平分线性质可得DM=PM,即可解题.
证明:(1)过N作NQ∥AD,则NQ=AD,AN=DQ,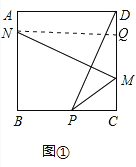
∵MN是PD垂直平分线,
∴DM=PM,
∵∠NMQ+∠MNQ=90°,∠NMQ+∠PDC=90°,
∴∠MNQ=∠PDC,
∵在△MNQ和△PDC中,
∠MQN=∠PCD=90°,NQ=CD,∠MNQ=∠PDC
∴△MNQ≌△PDC,(ASA)
∴QM=PC,
∵DM=DQ+QM,
∴PM=AN+PC,即PM-CP=AN;
(2)①M在图②位置时,不成立,新结论为AN=PM+CP;
理由:作MQ∥BF,则AQ=DM,QM=AD=CD,∠QMD=90°,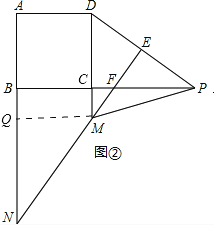
∵EF是PD垂直平分线,∴DM=PM,
∴PM=AQ,
∵∠NMQ+∠DME=90°,∠DME+∠MDE=90°,
∴∠NMQ=∠MDE,
∵在△NMQ和△PDC中,
∠NMQ=∠MDE,QM=CD,∠MQN=∠DCP=90°
∴△NMQ≌△PDC,(ASA)
∴QN=PC,
∵AN=AQ+QN,
∴AN=PM+CP;
②M在图③位置时,成立,
理由:作NQ∥BC,则NQ=AD=CD,AN=DQ,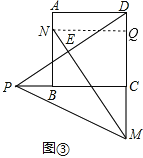
∵EM是PD的垂直平分线,
∴DM=PM,
∵∠NMD+∠MDE=90°,∠CPD+∠MDE=90°,
∴∠NMD=∠CPD,
∵在△CDP和△EDM中,
∠NMD=∠CPD,∠MQN=∠PCD,CD=NQ
∴△CDP≌△EDM,(AAS)
∴QM=CP,
∵DM=QM+DQ,
∴PM=AN+CP,即PM-CP=AN.


科目:初中数学 来源: 题型:
【题目】如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以_____________________∥_____________________ (同位角相等,两直线平行).
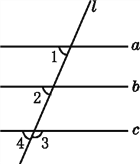
(2)因为∠3+∠4=180°(平角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4,
所以_________________∥_________________ (同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组中的四条线段成比例的是( )
A.a=1,b=3,c=2,d=4
B.a=4,b=6,c=5,d=10
C.a=2,b=4,c=3,d=6
D.a=2,b=3,c=4,d=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com