
分析 (1)由题可知m、n是方程x2+3x+c=0的两根,从而可得m2+3m+c=0,m+n=-3,将m3+3m2+(c-2)m-2n-c=8转化为m(m2+3m+c)-2(m+n)-c=8,就可求出c,即可得到抛物线的解析式,再根据抛物线与双曲线y=$\frac{k}{x}$的交点为(1,d),可求出d和k,即可得到双曲线的解析式;
(2)过点P1作直线a1∥x轴交y轴于A1,过Pn+1作直线bn+1∥y轴交x轴于Bn+1、交a1于Cn+1,如图,运用割补法可求得Sn=$n+\frac{n}{n+1}$.设Q(x1,y1),则有${y_1}=\frac{2}{x_1}$,即可得到$S={S_{△QMO}}=\frac{1}{2}|{x_1}|•|{y_1}|=1$,然后代入所求式子中,就可解决问题.
解答 解:(1)根据题意可得:
$\left\{\begin{array}{l}{m({m}^{2}+3m+c)-2(m+n)-c=8}\\{{m}^{2}+3m+c=0}\\{m+n=-3}\end{array}\right.$,
解得c=-2,
∴抛物线的解析式为y=x2+3x-2.
∵抛物线与双曲线y=$\frac{k}{x}$的交点为(1,d),
∴$\left\{\begin{array}{l}{d={1}^{2}+3×1-2}\\{d=\frac{k}{1}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{d=2}\\{k=2}\end{array}\right.$,
∴双曲线的解析式为y=$\frac{2}{x}$;
(2)∵点P1,P2,…,Pn+1都在双曲线y=$\frac{2}{x}$(x>0)上,它们的横坐标分别为a,2a,…,(n+1)a,
∴点P1,P2,…,Pn+1的纵坐标分别为$\frac{2}{a}$,$\frac{2}{2a}$,…,$\frac{2}{(n+1)a}$.
过点P1作直线a1∥x轴交y轴于A1,过Pn+1作直线bn+1∥y轴交x轴于Bn+1、交a1于Cn+1,如图,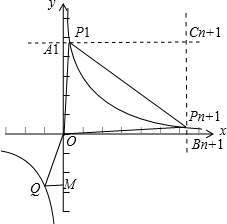
则Sn=SP1Pn+1O=(n+1)a•$\frac{2}{a}$-$\frac{1}{2}a•\frac{2}{a}$-$\frac{1}{2}(n+1)a•\frac{2}{(n+1)a}$-$\frac{1}{2}[(n+1)a-a][\frac{2}{a}-\frac{2}{(n+1)a}]$
=$n+\frac{n}{n+1}$.
设Q(x1,y1)(x1<0),则${y_1}=\frac{2}{x_1}$,
∴$S={S_{△QMO}}=\frac{1}{2}|{x_1}|•|{y_1}|=1$.
∴S1+S2+…+S2011+$\frac{S}{2}+\frac{S}{3}+…+\frac{S}{2012}$
=(1+$\frac{1}{2}$)+(2+$\frac{2}{3}$)+…+(2011+$\frac{2011}{2012}$)+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2012}$
=1+2+…+2011+$\frac{1}{2}$+$\frac{1}{2}$+$\frac{2}{3}$+$\frac{1}{3}$+…+$\frac{2011}{2012}$+$\frac{1}{2012}$
=1+2+…+2011+1×2011
=$\frac{(1+2011)×2011}{2}$+2011
=2025077.
点评 本题主要考查了抛物线与双曲线图象上点的坐标特征、根与系数的关系、方程解的定义等知识,对运算能力的要求比较高,技巧性强,如第(1)小题将m3+3m2+(c-2)m-2n-c=8巧妙地转化为m(m2+3m+c)-2(m+n)-c=8,第(2)小题运用割补法得到Sn=$n+\frac{n}{n+1}$,代入运算时,将整数与同分母的分数分别相加,并运用等差数列的求和公式求和.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
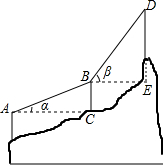 如图,AB=BD=100,AC⊥BC,BE⊥DE,∠α=16°,∠β=42°,求BC、AC、BE、DE.(sin16°≈0.28,cos16°≈0.96,tan16°≈0.29,sin42°≈0.67,cos42°≈0.74,tan42°≈0.9)
如图,AB=BD=100,AC⊥BC,BE⊥DE,∠α=16°,∠β=42°,求BC、AC、BE、DE.(sin16°≈0.28,cos16°≈0.96,tan16°≈0.29,sin42°≈0.67,cos42°≈0.74,tan42°≈0.9)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com