
 如图,在长方形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在线段AC上的点E、F处,折痕分别为CM、AN.
如图,在长方形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在线段AC上的点E、F处,折痕分别为CM、AN.分析 (1)欲证明DN=BM,只需推知△ADN≌△CBM即可.
(2)如图2中,作NH⊥AB于H.设DN=NF=x,则CN=4-x,CF=2,在Rt△NFC中,由CN2=CF2+NF2,列出方程求出x,在Rt△MNH中,求出NH、MH,根据MN=$\sqrt{H{N}^{2}+H{M}^{2}}$
计算即可.
(3)如图3中,连接EN,FM,首先证明四边形MENF是平行四边形,根据S△MNE=$\frac{1}{2}$S平行四边形MENF=S△EFN=$\frac{1}{2}$•EF•NF计算即可.
解答 (1)证明:如图1,由折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,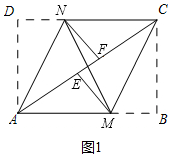
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DAN=∠BCM,
在Rt△ADN和Rt△CBM中,
$\left\{\begin{array}{l}{∠D=∠B=90°}\\{AD=BC}\\{∠DAM=∠BCM}\end{array}\right.$,
∴△ADN≌△CBM(ASA),
∴DN=BM;
(2)如图2中,作NH⊥AB于H.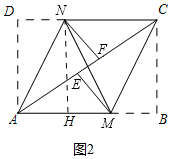
在Rt△ADC中,∵∠D=90°,AD=BC=3,CD=AB=4,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由折叠的性质得出可知,AD=AF=3,DN=NF,设DN=NF=x,则CN=4-x,CF=2,
在Rt△NFC中,∵CN2=CF2+NF2,
∴(4-x)2=x2+22,
∴x=$\frac{3}{2}$,
∴DN=NF=$\frac{3}{2}$,
∵∠D=∠DAH=∠AHN=90°,
∴四边形ADNH是矩形,
∴NH=AD=3,AH=DN=$\frac{3}{2}$,HM=AM-AH=4-$\frac{3}{2}$-$\frac{3}{2}$=1,
在Rt△MNH中,MN=$\sqrt{H{N}^{2}+H{M}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
(3)如图3中,连接EN,FM.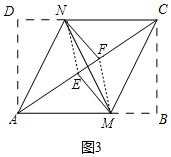
∵NF⊥AC,EM⊥AC,DN=NF=BM=EM,
∴NF∥EM,NF=EM,
∴四边形MENF是平行四边形,
∴S△MNE=$\frac{1}{2}$S平行四边形MENF=S△EFN=$\frac{1}{2}$•EF•NF=$\frac{1}{2}$×(6-5)×$\frac{3}{2}$=$\frac{3}{4}$.
点评 本题主要考查翻折变换的知识点,还涉及平行四边形的证明,解答(3)问的关键是证明四边形MENF是平行四边形,要熟练掌握此类试题的解答,此类题经常出现中考试卷中,请同学们关注.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
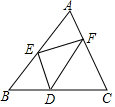 如图,已知D为△ABC的BC边上的一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:△AEF面积为△BDE面积和△CDF面积的比例中项.
如图,已知D为△ABC的BC边上的一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:△AEF面积为△BDE面积和△CDF面积的比例中项.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com