
【题目】如图,正方形![]() 的边长为6,
的边长为6,![]() 是边
是边![]() 上的一点,
上的一点,![]() 绕点
绕点![]() 逆时针旋转后得到
逆时针旋转后得到![]() .
.![]() 三点在同一直线上.
三点在同一直线上.
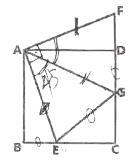
(1)求四边形![]() 的面积.
的面积.
(2)如果点![]() 在边
在边![]() 上,且
上,且![]() ,试判断
,试判断![]() 之间有什么样的数量关系?并说明理由.
之间有什么样的数量关系?并说明理由.
(3)在(2)的条件下,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)36;(2)GE=DG+BE,理由见解析;(3)![]() 的长为3.
的长为3.
【解析】
(1)由旋转的性质得△ABE≌△ADF,进而得出S四边形AECF=S正方形ABCD,计算即可;
(2)根据旋转的性质求出∠GAF=45°,然后利用SAS证明△AGE≌△AGF,得到GE=GF,等量代换即可求出GE=DG+BE;
(3)设DG=x,求出CG=6-x,EC=4,GE=x+2,然后在Rt△CEG中利用勾股定理构建方程,求出x即可.
解:(1)由旋转的性质得:△ABE≌△ADF,
∴![]() ,
,
∴S四边形AECF=S四边形AECD+S△ADF=S四边形AECD+S△ABE=S正方形ABCD=6×6=36;
(2)GE=DG+BE,
理由:由旋转的性质得:AE=AF,BE=DF,∠BAE=∠DAF,
在正方形ABCD中,∠BAD=90°,
∵∠GAE=45°,
∴∠BAE+∠GAD=45°,
∴∠DAF+∠GAD=45°,即∠GAF=45°,
在△AGE和△AGF中,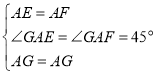 ,
,
∴△AGE≌△AGF(SAS),
∴GE=GF,
∵GF=DG+DF,BE=DF,
∴GE=DG+BE;
(3)设DG=x,则CG=6-x,
∵BE=DF=2,
∴EC=6-2=4,GE=GF=x+2,
在Rt△CEG中,∵EC2+CG2=GE2,
∴![]() ,
,
解得:x=3,
即![]() 的长为3.
的长为3.


科目:初中数学 来源: 题型:
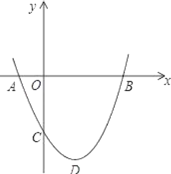
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为点D,其图象与x轴的交点A,B的横坐标分别为﹣1和3,给出下列结论:①2a﹣b=0;②a+b+c<0;③3a+c=0;④当a=![]() 时,△ABD是等腰直角三角形.其中,正确的结论有( )
时,△ABD是等腰直角三角形.其中,正确的结论有( )
A.①②③B.③④C.②③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
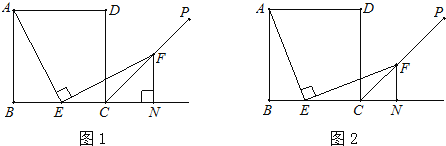
【题目】如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
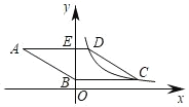
【题目】如图,在平面直角坐标系中,四边形 ABCD是菱形,BC∥x 轴.AD 与 y轴交于点 E,反比例函数 y=![]() (x>0)的图象经过顶点 C、D,已知点 C的横坐标为5,BE=2DE,则 k的值为( )
(x>0)的图象经过顶点 C、D,已知点 C的横坐标为5,BE=2DE,则 k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
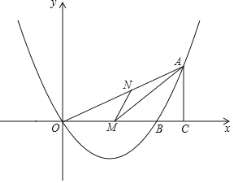
【题目】如图,已知二次函数 y=ax2+bx 的图象与 x 轴交于点 O(0,0)和 点 B,抛物线的对称轴是直线 x=3.点 A 是抛物线在第一象限上的一个动点, 过点 A 作 AC⊥x 轴,垂足为 C.S△AOB=3S△ABC,AC2=OCBC.
(1)求该二次函数的解析式;
(2)抛物线的对称轴与 x 轴交于点 M.连接 AM,点 N 是线段 OA 上的一点.当 ∠AMN=∠AOM 时,求点 N 的坐标;
(3)点 P 是抛物线上的一个动点.点 Q 是 y 轴上的一动点.当以 A,B,P,Q 四个点为顶点的四边形为平行四边形时,直接写出点 P 坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着第27届信阳茶文化节发布会、固始西九华山第三届郁金香风情文化节等系列活动的成功举办,越来越多的游客想要到信阳游玩小明所在的公司想在五一黄金周期间组织员工去信阳游玩,咨询了甲、乙两家旅行社,两家旅行社分别推出优惠方案(未推出优惠方案前两家旅行社的收费标准相同).甲:购买一张团体票,然后个人票打六折优惠;乙:不购买团体票,当团体人数超过一定数量后超过部分的个人票打折优惠,优惠期间,公司的员工人数为x(人),在甲旅行社所需总费用为![]() (元),在乙旅行社所需总费用为
(元),在乙旅行社所需总费用为![]() (元).
(元).![]() 、
、![]() 与x之间的函数关系如图所示.
与x之间的函数关系如图所示.
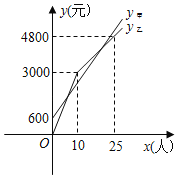
(1)甲旅行社团体票是______元,乙旅行社团体人数超过一定数量后,个人票打______折;
(2)求![]() 、
、![]() 关于x的函数表达式;
关于x的函数表达式;
(3)请说明小明所在的公司选择哪个旅行社出游更划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
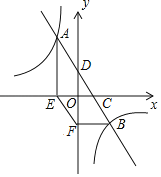
【题目】如图,已知一次函数y=﹣2x+b与反比例函数y=![]() 的图象有两个交点A(m,3)和B,且一次函数y=﹣2x+b与x轴、y轴分别交于点C、D.过点A作AE⊥x轴于点E;过点B作BF⊥y轴于点F,点F的坐标为(0,﹣2),连接EF,tan∠FEO=2.
的图象有两个交点A(m,3)和B,且一次函数y=﹣2x+b与x轴、y轴分别交于点C、D.过点A作AE⊥x轴于点E;过点B作BF⊥y轴于点F,点F的坐标为(0,﹣2),连接EF,tan∠FEO=2.
(1)求一次函数与反比例函数的解析式;
(2)求四边形AEFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过A(-1,0),B(3,0)与点C(0,3),连接BC,点P是直线BC是上方的一个动点(且不与B,C重合).
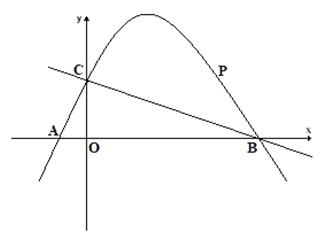
(1)求抛物线的解析式;
(2)求△PBC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
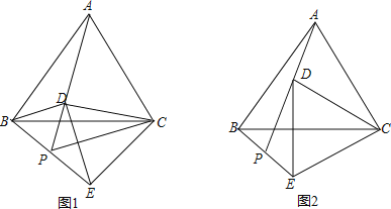
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com