
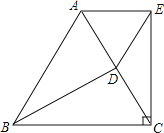
【题目】如图,已知△ABC是等边三角形,D是边AC的中点,连接BD,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.
【答案】详见解析.
【解析】
利用△ABC是等边三角形,D为边AC的中点,求得∠ADB=90°,再用SAS证明△CBD≌△ACE,推出AE=CD=AD,∠AEC=∠BDC=90°,根据直角三角形斜边上中线性质求出DE=AD,即可得出答案.
证明:∵△ABC是等边三角形,D为边AC的中点,
∴BD⊥AC,即∠ADB=90°,
∵EC⊥BC,
∴∠BCE=90°,
∴∠DBC+∠DCB=90°,∠ECD+∠BCD=90°,
∴∠ACE=∠DBC,
∵在△CBD和△ACE中
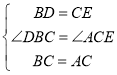
∴△CBD≌△ACE(SAS),
∴CD=AE,∠AEC=∠BDC=90°,
∵D为边AC的中点,∠AEC=90°,
∴AD=DE,
∴AD=AE=DE,
即△ADE是等边三角形,


科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,在平行四边形内作以线段AD为边的等边△ADM,连结AM.
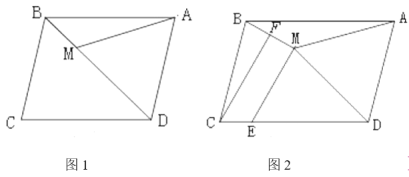
(1)如图1,若点M在对角线BD上,且∠ABC=105°,AB=![]() ,求AM的长;
,求AM的长;
(2)如图2,点E为CD边上一点,连接ME,点F是BM的中点,![]() ,若CE+ME=DE.求证:BM⊥ME.
,若CE+ME=DE.求证:BM⊥ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )
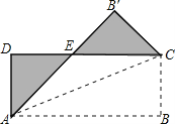
A.16B.19C.22D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=2x-2的图像与y轴交于点A,直线y2=-2x+6的图像与y轴交于点B,两者相交于点C.
(1)方程组![]() 的解是______;
的解是______;
(2)当y1>0与y2>0同时成立时,x的取值范围为_____;
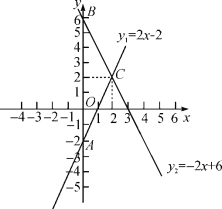
(3)求△ABC的面积;
(4)在直线y1=2x-2的图像上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
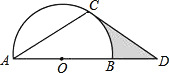
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点都在正方形网格的格点上,点
的顶点都在正方形网格的格点上,点![]()
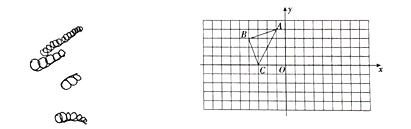
(1)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为___________.
的坐标为___________.
(2)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为__________.
的坐标为__________.
(3)观察图形,说一说点![]() 和点
和点![]() 的坐标有什么特点.
的坐标有什么特点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了________度,线段CE旋转过程中扫过的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做和美四边形,对角线交点称为和美四边形的中心.
(1)写出一种你学过的和美四边形_________;
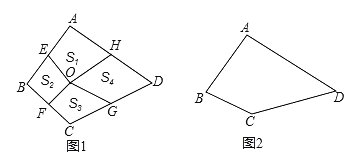
(2)如图1,点O是和美四边形ABCD的中心,E,F,G、H分别是边AB,BC,CD,DA的中点,连接OE,OF,OG,OH,记四边形AEOH,BEOF,CGOF,DHOG的面积为![]() ,用等式表示
,用等式表示![]() 的数量关系(无需说明理由).
的数量关系(无需说明理由).
(3)如图2,四边形ABCD是和美四边形,若AB=3,BC=2,CD=4,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com