
【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),点P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:过圆心C的任意直线CP与⊙C交于点A,B,若满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图点P为⊙C的一个“完美点”.
(1)当⊙O的半径为2时
①点M(![]() ,0) ⊙O的“完美点”,点(﹣
,0) ⊙O的“完美点”,点(﹣![]() ,﹣
,﹣![]() ) ⊙O的“完美点”;(填“是”或者“不是”)
) ⊙O的“完美点”;(填“是”或者“不是”)
②若⊙O的“完美点”P在直线y=![]() x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)设圆心C的坐标为(s,t),且在直线y=﹣2x+1上,⊙C半径为r,若y轴上存在⊙C的“完美点”,求t的取值范围.
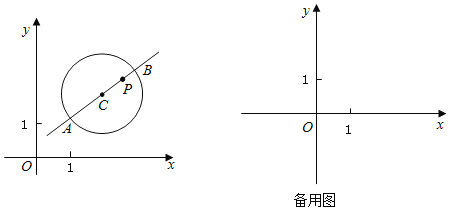
【答案】(1)①不是,是;②PO的长为1,点P的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );(2)t的取值范围为﹣1≤t≤3.
);(2)t的取值范围为﹣1≤t≤3.
【解析】
(1)①利用圆的“完美点”的定义直接判断即可得出结论.②先确定出满足圆的“完美点”的OP的长度,然后分情况讨论计算即可得出结论;(2)先判断出圆的“完美点”的轨迹,然后确定出取极值时OC与y轴的位置关系即可得出结论.
解:(1)①∵点M(![]() ,0),
,0),
∴设⊙O与x轴的交点为A,B,
∵⊙O的半径为2,
∴取A(﹣2,0),B(2,0),
∴|MA﹣MB|=|(![]() +2)﹣(2﹣
+2)﹣(2﹣![]() )|=3≠2,
)|=3≠2,
∴点M不是⊙O的“完美点”,
同理:点(﹣![]() ,﹣
,﹣![]() )是⊙O的“完美点”.
)是⊙O的“完美点”.
故答案为不是,是.
②如图1,
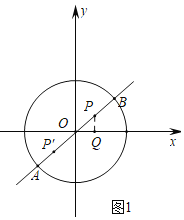
根据题意,|PA﹣PB|=2,
∴|OP+2﹣(2﹣OP)|=2,
∴OP=1.
若点P在第一象限内,作PQ⊥x轴于点Q,
∵点P在直线y=![]() x上,OP=1,
x上,OP=1,
∴![]() .
.
∴P(![]() ).
).
若点P在第三象限内,根据对称性可知其坐标为(﹣![]() ,﹣
,﹣![]() ).
).
综上所述,PO的长为1,点P的坐标为(![]() )或(
)或(![]() )).
)).
(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|=2,
∴|CP+r﹣(r﹣CP)|=2.
∴CP=1.
∴对于任意的点P,满足CP=1,都有|CP+r﹣(r﹣CP)|=2,
∴|PA﹣PB|=2,故此时点P为⊙C的“完美点”.
因此,⊙C的“完美点”是以点C为圆心,1为半径的圆.
设直线y=﹣2x+1与y轴交于点D,如图2,
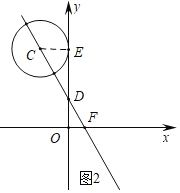
当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.
设切点为E,连接CE,
∵⊙C的圆心在直线y=﹣2x+1上,
∴此直线和y轴,x轴的交点D(0,1),F(![]() ,0),
,0),
∴OF=![]() ,OD=1,
,OD=1,
∵CE∥OF,
∴△DOF∽△DEC,
∴![]() ,
,
∴![]() ,
,
∴DE=2,
∴OE=3,
t的最大值为3,
当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
同理可得t的最小值为﹣1.
综上所述,t的取值范围为﹣1≤t≤3.


科目:初中数学 来源: 题型:
【题目】(8分)为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元?
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>0)支钢笔需要花y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕点C顺时针旋转a度(0°<a<180°)得到△DCE,点A与点D对应,点B与点E对应,当点D落在△ABC的边上时,则BD的长_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“弘扬传统文化,打造书香校园”的活动中,学校计划开展四项活动:“A﹣国学诵读”,“B﹣演讲”,“C﹣课本剧”,“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如图:
(1)如图,则被调查的总人数为 人;扇形统计图中,希望参加活动A所占圆心角为 度.
(2)根据题中信息补全条形统计图;
(3)学校现有1000名学生,请根据图中信息,估算全校学生希望参加活动D有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
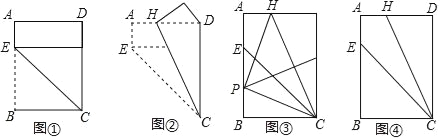
【题目】对给定的一张矩形纸片ABCD进行如下操作:先沿CE折叠,使点B落在CD边上(如图①),再沿CH折叠,这时发现点E恰好与点D重合(如图②)
(1)根据以上操作和发现,求![]() 的值;
的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点C与点H重合,折痕与AB相交于点P,再将该矩形纸片展开.求证:∠HPC=90°;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的P点,要求只有一条折痕,且点P在折痕上,请简要说明折叠方法.(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com