
【题目】今年4月份,某校九年级学生参加了广州市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
|
| 2 |
|
| 5 |
|
| 15 |
|
|
|
|
| 10 |
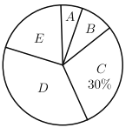
(1)求全班学生人数和![]() 的值.
的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本![]() (元)与月份
(元)与月份![]() (月)之间的关系可近似地表示为:
(月)之间的关系可近似地表示为:![]() ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为![]() (吨),每月的利润为
(吨),每月的利润为![]() (元).
(元).
(1)分别求出![]() 与
与![]() ,
,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)在今年内该单位哪个月获得利润达到5800元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上的一点,且
上的一点,且![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).

(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值.
的值.
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒2个单位长度的速度沿
上以每秒2个单位长度的速度沿![]() 往返运动,连结
往返运动,连结![]() 、
、![]() ,当点
,当点![]() 停止时点
停止时点![]() 也随之停止,直接写出矩形
也随之停止,直接写出矩形![]() 面积是
面积是![]() 面积的4倍时
面积的4倍时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,可是小红这两道题都不会,不过竞赛规则规定每位选手有两次求助机会,使用“求助”一次可以让主持人去掉其中一题的一个错误选项,主持人提醒小红可以使用两次“求助”.
(1)如果小红两次“求助”都在第一道题中使用,那么小红通关的概率是 .
(2)如果小红将每道题各用一次“求助”,请用树状图或者列表来分析她顺序通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
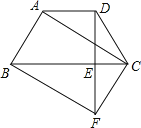
【题目】如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CD、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
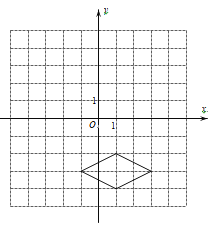
【题目】在平面直角坐标系中,x轴下方有一个菱形,如图所示,画图并回答问题.
(1)将x轴下方的菱形先向右平移2个单位长度,再向上平移6个单位长度,画出平移后的图形;
(2)将x轴下方的菱形绕着原点顺时针方向旋转 90°,画出旋转后的图形;
(3)在(1)和(2)中画出的两个图形存在一种特殊关系,即一个图形绕着某点旋转一个角度可以得到另一个图形,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.
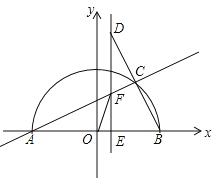
(1)当∠BAC=30时,求△ABC的面积;
(2)当DE=8时,求线段EF的长;
(3)在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
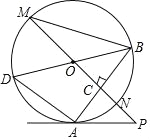
【题目】如图,已知⊙O中,AB为弦,直线PO交⊙O于点M、N,PO⊥AB于C,过点B作直径BD,连接AD、BM、AP.
(1)求证:PM∥AD;
(2)若∠BAP=2∠M,求证:PA是⊙O的切线;
(3)若AD=6,tan∠M=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com