
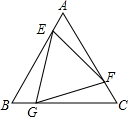
 等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.
等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$. 分析 由于△BEG、△CGF、△AEF是全等的,所以只要求出其中一个三角形的面积就可求出△EFG的面积.连接EC,可得△BEC的面积是△ABC面积的五分之四,△BEG的面积是△BEC面积的五分之一.
解答 解:连接EC,如图,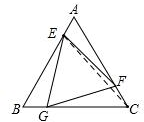
∵E点是AB的五等分点,
∴${S}_{△BCE}=\frac{4}{5}{S}_{△ABC}=\frac{4}{5}$,
∵G点是BC的五等分点,
∴${S}_{△BEG}=\frac{1}{5}{S}_{△BCE}=\frac{4}{25}$,
同理:${S}_{△CGF}={S}_{△AEF}=\frac{4}{25}$,
∴S△GEF=S△ABC-3S△BEG=$\frac{13}{25}$.
故答案为$\frac{13}{25}$.
点评 本题主要考查了等积变换,难度不大,属于基础题.若两个三角形的高相同,则面积之比等于底之比,这是原理是解答本题的关键.


科目:初中数学 来源:2017届辽宁省大石桥市中考模拟(一)数学试卷(解析版) 题型:判断题
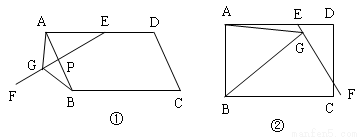
如图,在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作射线EF,在EF上取一点G,使∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为( )
A. (9,0) B. (﹣1,0) C. (3,﹣1) D. (﹣3,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
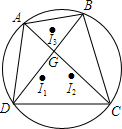 如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=-2 | D. | a=-1,b=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com