
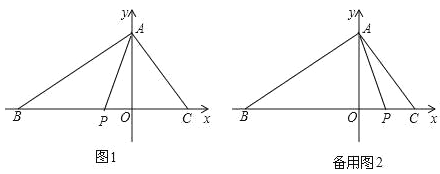
【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(-5,0),且![]() ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.

(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出Q点坐标;若不存在,请说明理由.
【答案】(1)A的坐标是(0,4),C的坐标是(3,0);(2)当0≤t<![]() 时,s=10-4t;当t=
时,s=10-4t;当t=![]() 时,s=0;当t>
时,s=0;当t>![]() 时,
时,
【解析】
试题分析:(1)根据偶次方和算术平方根的非负性得出n-3=0,3m-12=0,求出即可;
(2)分为三种情况:当0≤t<![]() 时,P在线段OB上,②当t=
时,P在线段OB上,②当t=![]() 时,P和O重合,③当t>
时,P和O重合,③当t>![]() 时,P在射线OC上,求出OP和OA,根据三角形的面积公式求出即可;
时,P在射线OC上,求出OP和OA,根据三角形的面积公式求出即可;
(3)分为四种情况:①当BP=1,OQ=3时,②当BP=2,OQ=4时,③④利用图形的对称性直接写出其余的点的坐标即可.
试题解析:(1)∵![]() ,
,
∴n-3=0,3m-12=0,
n=3,m=4,
∴A的坐标是(0,4),C的坐标是(3,0);
(2)∵B(-5,0),
∴OB=5,
①当0≤t<![]() 时,P在线段OB上,如图1,
时,P在线段OB上,如图1,
∵OP=5-2t,OA=4,
∴△POA的面积S=![]() ×OP×AP=
×OP×AP=![]() ×(5-2t)×4=10-4t;
×(5-2t)×4=10-4t;
②当t=![]() 时,P和O重合,此时△APO不存在,即S=0;
时,P和O重合,此时△APO不存在,即S=0;
③当t>![]() 时,P在射线OC上,如备用图2,
时,P在射线OC上,如备用图2,
∵OP=2t-5,OA=4,
∴△POA的面积S=![]() ×OP×AP=
×OP×AP=![]() ×(2t-5)×4=4t-10;
×(2t-5)×4=4t-10;
(3)当P在线段BO上运动时,在y轴上存在点Q,使△POQ与△AOC全等,
∵P在线段BO上运动,
∴t≤5÷2=2.5,
①当BP=1,OQ=3时,△POQ和△AOC全等,
此时t=![]() ,Q的坐标是(0,3);
,Q的坐标是(0,3);
②当BP=2,OQ=4时,△POQ和△AOC全等,
此时t=![]() =1,Q的坐标是(0,4);
=1,Q的坐标是(0,4);
③④由对称性可知Q为(0,-3)、(0,-4)
综上所述,t=![]() 或1时,Q的坐标是(0,3)或(0,4)或(0,-3)或(0,-4).
或1时,Q的坐标是(0,3)或(0,4)或(0,-3)或(0,-4).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
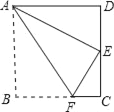
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求证:平行四边形ABCD是矩形;
(2)求BF的长;
(3)求折痕AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)

(1)在平面直角坐标系中描出点A,B,C,并画△ABC;
(2)将△ABC向左平移3个单位后再向下平移2个单位,得到△A1B1C1,请在平面直角坐标系中画出△A1B1C1;
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列命题中,是假命题的个数有( )
①如果![]() ,那么
,那么![]() . ② 两条直线被第三条直线所截,同位角相等
. ② 两条直线被第三条直线所截,同位角相等
③面积相等的两个三角形全等 ④ 三角形的一个外角等于不相邻的两个内角的和.
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为10m,求塑像的高度CF.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com