
分析 (1)先化简,后根据多项式不含二次项可确定出a、b的值;
(2)分两种情况,当C在A,B之间,当C在B的右边,求得AB+BC的值,即可得到结论.
解答 解:(1)原式=ax2+3axy-2x-5+bxy+2x2-5x-6
=(a+2)x2+(3a+b)xy-7x-11.
∵多项式不含二次项,
∴a=-2,b=6.
∴点A表示的数是-2,点B表示的数是6,
故答案为:-2,6.
(2)设运动时间为t,
当C在A,B之间,
∵AB+BC=6+t-(-2-3t)+(6+t-5t)=14,
∴线段AB+BC的值不变,
当C在B的右边,∵AB+BC=6+t-(-2-3t)+(5t-6-t)=8t+2,
∴线段AB+BC的值随运动时间变化.
点评 本题考查了多项式,数轴,熟记多项式和数轴的概念是解题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数x | 余额y(元) |
| 1 | 100-1.6 |
| 2 | 100-3.2 |
| 3 | 100-4.8 |
| 4 | 100-6.4 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
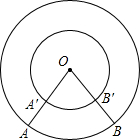 如图,两个同心圆的圆心为点O,A,B是最大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,那么( )
如图,两个同心圆的圆心为点O,A,B是最大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,那么( )| A. | $\widehat{AB}$=$\widehat{A′B′}$ | B. | $\widehat{AB}$>$\widehat{A′B′}$ | ||
| C. | $\widehat{AB}$的度数等于$\widehat{A′B′}$的度数 | D. | $\widehat{AB}$的长度等于$\widehat{A′B′}$的长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com