
已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8﹣4
 ,求正方形ABCD的面积?
,求正方形ABCD的面积?


【考点】正方形的性质;全等三角形的判定与性质;勾股定理.
【分析】(1)利用正方形的性质,由全等三角形的判定定理SAS即可证得△BCE≌△DCF;
(2)首先证明△BDG≌△BGF,从而得到OG是△DBF的中位线,即可得出答案;
(3)设BC=x,则DC=x,BD=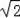
 x,由△BGD≌△BGF,得出BF=BD,CF=(
x,由△BGD≌△BGF,得出BF=BD,CF=(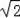
 ﹣1)x,利用勾股定理DF2=DC2+CF2,解得x2=2,即正方形ABCD的面积是2.
﹣1)x,利用勾股定理DF2=DC2+CF2,解得x2=2,即正方形ABCD的面积是2.
【解答】解:(1)证明:在△BCE和△DCF中,
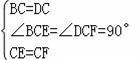
 ,
,
∴△BCE≌△DCF(SAS);
(2)OG∥BF且OG=
 BF,
BF,
理由:如图,


∵BE平分∠DBC,
∴∠2=∠3,
在△BGD和△BGF中,
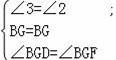
 ,
,
∴△BGD≌△BGF(ASA),
∴DG=GF,
∵O为正方形ABCD的中心,
∴DO=OB,
∴OG是△DBF的中位线,
∴OG∥BF且OG=
 BF;
BF;
(3)设BC=x,则DC=x,BD=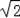
 x,由(2)知△BGD≌△BGF,
x,由(2)知△BGD≌△BGF,
∴BF=BD,
∴CF=(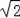
 ﹣1)x,
﹣1)x,
∵DF2=DC2+CF2,
∴x2+[(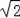
 ﹣1)x]2=8﹣4
﹣1)x]2=8﹣4
 ,解得x2=2,
,解得x2=2,
∴正方形ABCD的面积是2.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
某超市销售一种饮料,平均每天可售出100箱,每箱利润120元。天气渐热,为了扩大
销售,增加利润,超市准备适当降价。据测算,若每箱饮料每降价1元,每天可多售出2箱。针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,
问每箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程(m﹣1)x2+x+m2+4m﹣5=0的一个根为0,则m的值为( )
A.1 B.﹣5 C.1或﹣5 D. m≠1的任意实数
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[﹣π]=﹣4.
(1)如果[a]=﹣2,那么a的取值范围是 .
(2)如果[
 ]=3,求满足条件的所有正整数x.
]=3,求满足条件的所有正整数x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com