
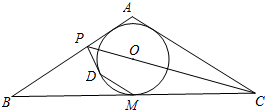
 已知等腰△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙O与BC边的切点,作MD∥AC,交⊙O于点D.
已知等腰△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙O与BC边的切点,作MD∥AC,交⊙O于点D.分析 (1)连接AM,根据⊙O是△ABC的内切圆,且AB=AC可得A、O、M 三点共线,AM⊥BC.再由CP是∠ACB的平分线得出∠ACP=∠BCP.设∠BCP=α,由直角三角形的性质可知∠COM=90°-α.∠AOP=∠COM=90°-α.设AB切⊙O于F,连接OF,则OF⊥AB.故∠BAM=90°-2α,根据DM∥AC可用α表示出∠DOM的度数,连接OD,由三角形内角和定理可得出∠POD=90°-3α,故∠FOP=∠DOP.根据SAS定理可得出△FOP≌△DOP,由此可得出结论;
(2)在直角三角形ABM中,sin∠B=$\frac{AM}{AB}$=$\frac{3}{5}$可得出AM及BM的长,由三角形的面积公式可得出OM的长,由勾股定理可求出OC的长.
解答 (1)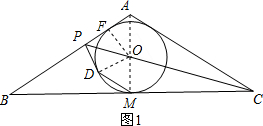 证明:方法一:如图1,连接AM.
证明:方法一:如图1,连接AM.
∵⊙O是△ABC的内切圆,且AB=AC,
∴A、O、M 三点共线,AM⊥BC.
又∵CP是∠ACB的平分线,
∴∠ACP=∠BCP.
设∠BCP=α,则∠COM=90°-α.
∴∠AOP=∠COM=90°-α.
设AB切⊙O于F,连接OF,则OF⊥AB.
又∠BAM=90°-2α,
∴∠AOF=2α.
∴∠FOP=90°-3α.
又∵DM∥AC,
∴∠DMB=∠ACB=2α.
∴∠DOM=180°-2×(90°-2α)=4α.
连接OD,则∠POD=180°-4α-(90°-α)=90°-3α.
∴∠FOP=∠DOP.
在△FOP与△DOP中,
$\left\{\begin{array}{l}{OF=OD}\\{∠FOP=∠DOP}\\{OP=OP}\end{array}\right.$
∴△FOP≌△DOP(SAS).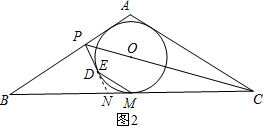
∴∠PDO=∠PFO=90°.
∴OD⊥PD.
∴PD为⊙O的切线.
方法二:过点P作⊙O的切线PE(切点为E)并延长,交BC于点N.
∵CP为∠ACB的平分线,
∴∠ACP=∠BCP.
又∵PA、PE均为⊙O的切线,
∴∠APC=∠NPC.
在△ACP与△NCP中,
$\left\{\begin{array}{l}∠ACP=∠BCP\\∠APC=∠NPC\\ CP=CP\end{array}\right.$,
∴△ACP≌△NCP(AAS),
∴∠PAC=∠PNC.
∵NM=NE,AB=AC,
∴$\frac{NE}{BA}=\frac{NM}{AC}$.
∴△ENM∽△BAC.
∴∠NME=∠BCA.
∴ME∥AC.
又∵MD∥AC,
∴MD和ME为同一条直线.
又点E、D均在⊙O上,所以点E和点D重合,故PD是⊙O的切线.
(2)∵在直角三角形ABM中,sin∠B=$\frac{AM}{AB}=\frac{3}{5}$,AB=5,
∴AM=3.
∴BM=4.
∴BC=2BM=8.
由△ABC面积,得$\frac{1}{2}$BC•AM=$\frac{1}{2}$OM•(AB+BC+CA).
即$\frac{1}{2}$×8×3=$\frac{1}{2}$×ON×(5+8+5).
解得OM=$\frac{4}{3}$.
∴OC=$\sqrt{O{M}^{2}+C{M}^{2}}$=$\frac{4\sqrt{10}}{3}$.
点评 本题考查的是圆的综合题,涉及到全等三角形的判定与性质、切线的性质及直角三角形的性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
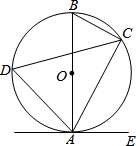 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
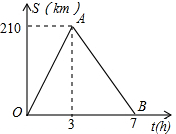 小明从A地出发,途中经过C地,后到达B地,到达B地后,立即原路返回,他距A地的距离S(千米)和所用时间t(小时)之间的函数关系如图所示,若小明前后两次经过点C时间相差2$\frac{1}{3}$小时,那么A、C两地之间距离为140千米.
小明从A地出发,途中经过C地,后到达B地,到达B地后,立即原路返回,他距A地的距离S(千米)和所用时间t(小时)之间的函数关系如图所示,若小明前后两次经过点C时间相差2$\frac{1}{3}$小时,那么A、C两地之间距离为140千米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com