
【题目】已知关于x的方程![]() 有两个正整数根
有两个正整数根![]() 是正整数
是正整数![]() 的三边a、b、c满足
的三边a、b、c满足![]() ,
,![]() ,
,![]() .
.
求:![]() 的值;
的值;
![]() 的面积.
的面积.
【答案】![]() m=2
m=2![]() 1或
1或![]()
【解析】
(1)本题可先求出方程(m2-1)x2-3(3m-1)x+18=0的两个根,然后根据这两个根都是正整数求出m的值.
(2)由(1)得出的m的值,然后将m2+a2m-8a=0,m2+b2m-8b=0.进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
![]() 关于x的方程
关于x的方程![]() 有两个正整数根
有两个正整数根![]() 是整数
是整数![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,![]() 是此方程的两个根,
是此方程的两个根,
![]() ,
,
![]() 也是正整数,即
也是正整数,即![]() 或2或3或6或9或18,
或2或3或6或9或18,
又m为正整数,
![]() ;
;
![]() 把
把![]() 代入两等式,化简得
代入两等式,化简得![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,a、b是方程
时,a、b是方程![]() 的两根,而
的两根,而![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() ,则
,则![]() 、
、![]() .
.
![]() ,
,![]() 时,由于
时,由于![]()
故![]() 为直角三角形,且
为直角三角形,且![]() ,
,![]() .
.
![]() ,
,![]() 时,因
时,因![]() ,故不能构成三角形,不合题意,舍去.
,故不能构成三角形,不合题意,舍去.
![]() ,
,![]() 时,因
时,因![]() ,故能构成三角形.
,故能构成三角形.
![]()
综上,![]() 的面积为1或
的面积为1或![]() .
.


科目:初中数学 来源: 题型:
【题目】武汉市光谷实验中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),下列说法错误的是( )

A. 九(1)班的学生人数为40 B. m的值为10
C. n的值为20 D. 表示“足球”的扇形的圆心角是70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.
①△OBC与△ABD全等吗?判断并证明你的结论;
②当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾地区的D、E两县.根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨.
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍.其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨.则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
A地 | B地 | C地 | |
运往D县的费用(元/吨) | 220 | 200 | 200 |
运往E县的费用(元/吨) | 250 | 220 | 210 |
为及时将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
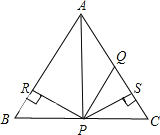
【题目】如图所示,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
,![]() 于R,
于R,![]() 于S,则四个结论正确的是
于S,则四个结论正确的是![]()
![]()
![]() 点P在
点P在![]() 的平分线上;
的平分线上;
![]() ;
;
![]() ;
;
![]() ≌
≌![]() .
.
A. 全部正确 B. 仅![]() 和
和![]() 正确 C. 仅
正确 C. 仅![]() 正确 D. 仅
正确 D. 仅![]() 和
和![]() 正确
正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是以原点为圆心, ![]() 为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )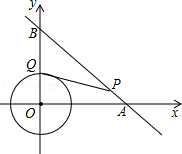
A.3
B.4
C.6﹣ ![]()
D.3 ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 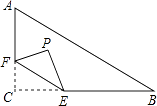
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:3+2=3×2﹣1,4+![]() =4×
=4×![]() ﹣1,给出定义如下:
﹣1,给出定义如下:
我们称使等式a+b=ab﹣1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(﹣2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(﹣n,﹣m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对”
(注意:不能与题目中已有的“椒江有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N. 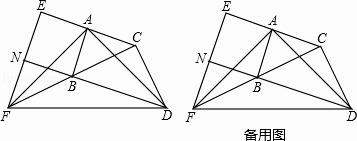
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com