
【题目】若二次函数y=kx2+(3k+2)x+2k+2.
(1)求证:抛物线与x轴有交点.
(2)经研究发现,无论k为何值,抛物线经过某些特定的点,请求出这些定点.
(3)若y1=2x+2,在﹣2<x<﹣1范围内,请比较y1,y的大小.
【答案】(1)见解析;(2)(﹣1,0)、(﹣2,﹣2);(3)当k>0时,y1>y;当k<0时,y1<y
【解析】
(1)令kx2+(3k+2)x+2k+2=0,只要根的判别式大于等于0恒成立即可;
(2)由y=kx2+(3k+2)x+2k+2=k(x2+3x+2)+2x+2,当x2+3x+2=0,-2x-2+y=0时,函数过定点,x=-1或x=-2,将其代入,即可求得定点坐标;
(3)根据函数图像,即可得到答案.
(1)△=b2﹣4ac=(3k+2)2﹣4k(2k+2)=(k+2)2≥0,
∴抛物线与x轴有交点;
(2)由y=kx2+(3k+2)x+2k+2=k(x2+3x+2)+2x+2,
得k(x2+3x+2)=-2x-2+y
当x2+3x+2=0,-2x-2+y=0时,函数过定点,则x=﹣1,y=0或x=﹣2,y=-2则定点为:(﹣1,0)、(﹣2,﹣2);
(3)如图所示,抛物线过定点:(﹣1,0)、(﹣2,﹣2),
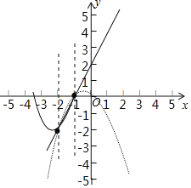
由图像可知:当k>0时,y1>y;
当k<0时,y1<y.


科目:初中数学 来源: 题型:
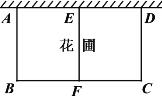
【题目】学校要围一个矩形花圃, 其一边利用足够长的墙, 另三边用篱笆围成, 由于园艺需要, 还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示), 总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD), 矩形花圃ABCD 的面积为S平方米.
(1)求S与![]() 之间的函数关系式, 并直接写出自变量
之间的函数关系式, 并直接写出自变量![]() 的取值范围;
的取值范围;
(2)要想使矩形花圃ABCD的面积最大, AB边的长应为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请求出y与x之间的函数关系式.
(2)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
(3)如果每天获得不低于160元的利润,销售单价范围是多少?至少出售多少袋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
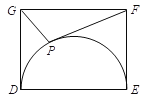
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
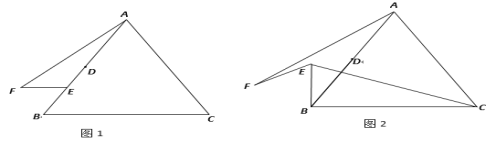
【题目】如图,在边长为8的等边△ABC中,点D是AB的中点,点E是平面上一点,且线段DE=2,将线段EB绕点E顺时针旋转60得到线段EF,连接AF.
(1)如图1,当BE=2时,求线段AF的长;
(2)如图2,求证:AF=CE;
查看答案和解析>>
科目:初中数学 来源: 题型:
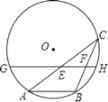
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为8,则GE+FH的最大值为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
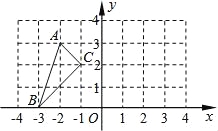
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com