
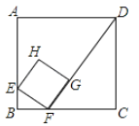
【题目】如图,边长12的正方形ABCD中,F为BC上一点,有一个小正方形EFGH,其中E、G分别在AB、FD上.若BF=3,则AH的长为____.
【答案】![]()
【解析】
由在边长为12的正方形ABCD中,有一个小正方形EFGH,根据同角的余角相等,可得∠BFE=∠CDF,继而证得△BEF∽△CFD,然后由相似三角形的对应边成比例,求得BE长,过H作HM⊥AB于M,则∠HMA=∠HME=90°,求出MH和AM长,再根据勾股定理求出即可.
四边形ABCD是正方形,
∴∠B=∠C=90°,
在△BEF与△CFD中,
∵∠BFE+∠CFD=∠CFD+∠CDF=90°,
∴∠BFE=∠CDF,
∴△BEF∽△CFD,
∴![]() =
=![]() ,
,
∵BF=3,BC=12,
∴CF=BC-BF=12-3=9,
∴![]() =
=![]() ,
,
∴BE=![]() ,
,
过H作HM⊥AB于M,
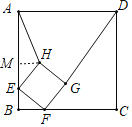
则∠HMA=∠HME=90°,
∵四边形ABCD和四边形EHGF是正方形,
∴∠HME=∠B=90°,EH=EF,∠HEF=90°,
∴∠MEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠MEH=∠EFB,
在△HME和△EBF中,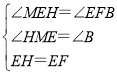 ,
,
∴△HME≌△EBF(AAS),
∴HM=BE=![]() ,ME=BF=3,
,ME=BF=3,
∴AM=AB-EM-BE=12-3-![]() =
=![]() ,
,
在Rt△AMH中,由勾股定理得:AH=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G时代即将来临,湖北省提出“建成全国领先、中部一流5G网络”的战略目标.据统计,目前湖北5G基站的数量有1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.
(1)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率;
(2)若2023年保持前两年5G基站数量的年平均增长率不变,到2023年底,全省5G基站数量能否超过29万座?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
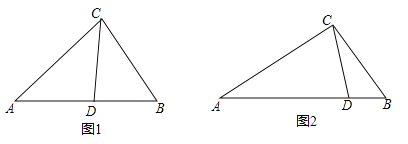
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④当m为任意实数时,a﹣b<am2+bm;⑤若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑥a>![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
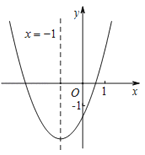
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=kx2+(3k+2)x+2k+2.
(1)求证:抛物线与x轴有交点.
(2)经研究发现,无论k为何值,抛物线经过某些特定的点,请求出这些定点.
(3)若y1=2x+2,在﹣2<x<﹣1范围内,请比较y1,y的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图象过点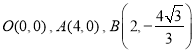 ,
,![]() 是
是![]() 中点.
中点.
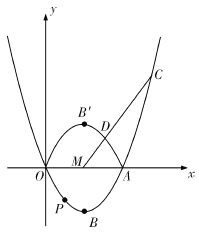
(1)求此二次函数的解析式.
(2)已知![]() ,点
,点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当
轴上,当![]() 四点构成以
四点构成以![]() 为边的平行四边形,求此时
为边的平行四边形,求此时![]() 点的坐标.
点的坐标.
(3)将抛物线在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴向上翻折,得曲线
轴向上翻折,得曲线![]() (
(![]() 为
为![]() 关于
关于![]() 轴的对称点),在原抛物线
轴的对称点),在原抛物线![]() 轴的上方部分取一点,连接
轴的上方部分取一点,连接![]() ,
,![]() 与翻折后的曲线
与翻折后的曲线![]() 交于点
交于点![]() . 若
. 若![]() 的面积是
的面积是![]() 面积的3倍,这样的点
面积的3倍,这样的点![]() 是否存在?若存在,求出
是否存在?若存在,求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有____________(只填序号).
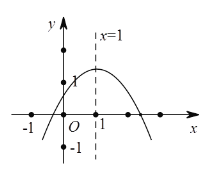
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com