
【题目】在平面直角坐标系中,O是坐标原点,抛物线y=﹣x2﹣2x+4交y轴于点B,过点B作AB∥x轴交抛物线于点A,连接OA.将该抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),则m的取值范围是( )
A. 1<m<5 B. 1<m<4 C. 1<m<3 D. 1<m<2
【答案】C
【解析】
设原抛物线的顶点为D,过点D作DE⊥AB于点E交AO于点F.先根据抛物线的解析式求出点B的坐标,再利用对称性求出点A的坐标,再利用二次函数的顶点坐标,根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围.
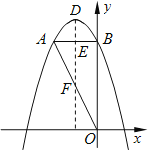
解:如图,设原抛物线的顶点为D,过点D作DE⊥AB于点E交AO于点F.
∵y=﹣x2﹣2x+4=﹣(x+1)2+5,
∴B(0,4),D(﹣1,5),对称轴为直线x=﹣1,
∵AB∥x轴交抛物线于点A,
∴A的坐标(﹣2,4),
∴AB的中点E的坐标是(﹣1,4),
∵OA的中点是F,
∴F的坐标是(﹣1,2),
当D点平移到E点时,平移后得到的抛物线顶点不在△OAB的内部,再继续往下平移正好进入△OAB的内部,
当D点平移到F点时,平移后得到的抛物线顶点正好不在△OAB的内部,
∴m的取值范围是:1<m<3.
故选:C.


科目:初中数学 来源: 题型:
【题目】炮弹的运行轨道若不计空气阻力是一条抛物线.现测得我军炮位A与射击目标B的水平距离为600m,炮弹运行的最大高度为1200m.
(1)求此抛物线的解析式;
(2)若在A、B之间距离A点500m处有一高350m的障碍物,计算炮弹能否越过障碍物.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
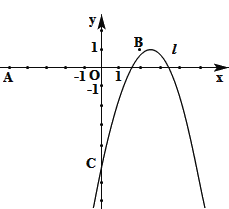
【题目】如图,已知点O (0,0),A (-5,0),B (2,1),抛物线![]() (h为常数)与y轴的交点为C。
(h为常数)与y轴的交点为C。
(1) 抛物线经过点B,求它的解析式,并写出此时抛物线的对称轴及顶点坐标;
(2)设点C的纵坐标为![]() ,求
,求![]() 的最大值,此时抛物线上有两点
的最大值,此时抛物线上有两点![]() ,
,![]() ,其中
,其中![]() ,比较
,比较![]() 与
与![]() 的大小;
的大小;
(3)当线段OA被只分为两部分,且这两部分的比是1:4时,求h的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
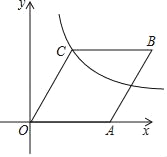
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,∠B=60°,反比例函数y=![]() (k>0)的图象经过点C,若将菱形向下平移2个单位,点B恰好落在反比例函数的图象上,则反比例函数的表达式为( )
(k>0)的图象经过点C,若将菱形向下平移2个单位,点B恰好落在反比例函数的图象上,则反比例函数的表达式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
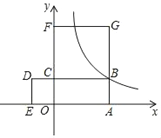
【题目】如图,点B是反比例函数图象上的一点,矩形OABC的周长是16,正方形BCFG和正方形OCDE的面积之和为32,则反比例函数的解析式为( )
A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与反比例函数的图象交于点A(1,3),B(3,1)两点,当一次函数大于反比例函数的值时,x的取值范围是( )
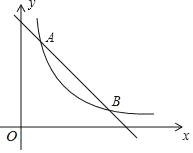
A. x<1 B. 1<x<3 C. x>3 D. x>4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com