
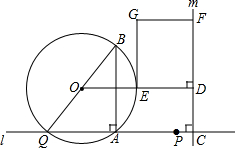
 如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=$\frac{3}{2}$CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=$\frac{3}{2}$CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.分析 (1)由AQ:AB=3:4,AQ=3x,易得AB=4x,由勾股定理得BQ,再由中位线的性质得AH=BH=$\frac{1}{2}$AB,求得CD,FD;
(2)利用(1)的结论,易得CQ的长,作OM⊥AQ于点M(如图1),则OM∥AB,由垂径定理得QM=AM=$\frac{3}{2}$x,由矩形性质得OD=MC,利用矩形面积,求得x,得出结论;
(3)①点P在A点的右侧时(如图1),利用(1)(2)的结论和正方形的性质得2x+4=3x,得AP;点P在A点的左侧时,当点C在Q右侧,0<x<$\frac{4}{7}$时(如图2),4-7x=3x,解得x,易得AP;当$\frac{4}{7}≤x<\frac{2}{3}$时(如图3),7-4x=3x,得AP;当点C在Q的左侧时,即x≥$\frac{2}{3}$(如图4),同理得AP;
②连接NQ,由点O到BN的弦心距为l,得NQ=2,当点N在AB的左侧时(如图5),过点B作BM⊥EG于点M,GM=x,BM=x,易得∠GBM=45°,BM∥AQ,易得AI=AB,求得IQ,由NQ得AP;当点N在AB的右侧时(如图6),过点B作BJ⊥GE于点J,由GJ=x,BJ=4x得tan∠GBJ=$\frac{1}{4}$,利用(1)(2)中结论得AI=16x,QI=19x,
解得x,得AP.
解答 解:(1)在Rt△ABQ中,
∵AQ:AB=3:4,AQ=3x,
∴AB=4x,
∴BQ=5x,
∵OD⊥m,m⊥l,
∴OD∥l,
∵OB=OQ,
∴$AH=BH=\frac{1}{2}AB$=2x,
∴CD=2x,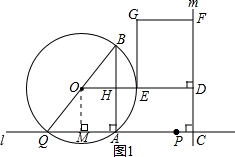 ∴FD=$\frac{3}{2}CD$=3x;
∴FD=$\frac{3}{2}CD$=3x;
(2)∵AP=AQ=3x,PC=4,
∴CQ=6x+4,
作OM⊥AQ于点M(如图1),
∴OM∥AB,
∵⊙O是△ABQ的外接圆,∠BAQ=90°,
∴点O是BQ的中点,
∴QM=AM=$\frac{3}{2}$x
∴OD=MC=$\frac{9}{2}x+4$,
∴OE=$\frac{1}{2}$BQ=$\frac{5}{2}x$,
∴ED=2x+4,
S矩形DEGF=DF•DE=3x(2x+4)=90,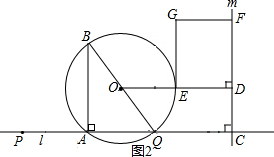 解得:x1=-5(舍去),x2=3,
解得:x1=-5(舍去),x2=3,
∴AP=3x=9;
(3)①若矩形DEGF是正方形,则ED=DF,
I.点P在A点的右侧时(如图1)
∴2x+4=3x,解得:x=4,
∴AP=3x=12;
II.点P在A点的左侧时,
当点C在Q右侧,
0<x<$\frac{4}{7}$时(如图2),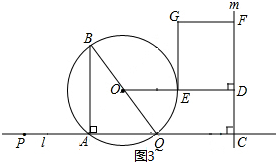 ∵ED=4-7x,DF=3x,
∵ED=4-7x,DF=3x,
∴4-7x=3x,解得:x=$\frac{2}{5}$,
∴AP=$\frac{6}{5}$;
当$\frac{4}{7}$≤x<$\frac{2}{3}$时(如图3),
∵ED=4-7x,DF=3x,
∴4-7x=3x,解得:x=$\frac{2}{5}$(舍去),
当点C在Q的左侧时,即x≥$\frac{2}{3}$(如图4),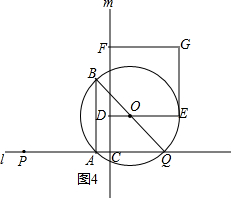 DE=7x-4,DF=3x,
DE=7x-4,DF=3x,
∴7x-4=3x,解得:x=1,
∴AP=3,
综上所述:当AP为12或$\frac{6}{5}$或3时,矩形DEGF是正方形;
②连接NQ,由点O到BN的弦心距为l,得NQ=2,
当点N在AB的左侧时(如图5),
过点B作BM⊥EG于点M,
∵GM=x,BM=x,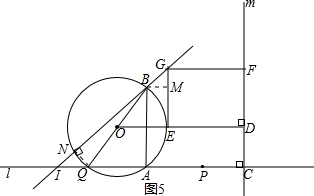
∴∠GBM=45°,
∴BM∥AQ,
∴AI=AB=4x,
∴IQ=x,
∴NQ=$\frac{x}{\sqrt{2}}$=2,
∴x=2$\sqrt{2}$,
∴AP=6$\sqrt{2}$;
当点N在AB的右侧时(如图6), 过点B作BJ⊥GE于点J,
过点B作BJ⊥GE于点J,
∵GJ=x,BJ=4x,
∴tan∠GBJ=$\frac{1}{4}$,
∴AI=16x,
∴QI=19x,
∴NQ=$\frac{19x}{\sqrt{17}}$=2,
∴x=$\frac{2\sqrt{17}}{19}$,
∴AP=$\frac{6\sqrt{17}}{19}$,
综上所述:AP的长为6$\sqrt{2}$或$\frac{6\sqrt{17}}{19}$.
点评 本题主要考查了勾股定理,垂径定理,正方形的性质,中位线的性质等,结合图形,分类讨论是解答此题的关键.


科目:初中数学 来源: 题型:选择题
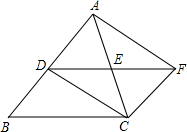 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 任意四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
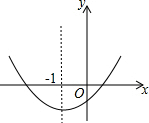 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:| A. | ①② | B. | 只有① | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
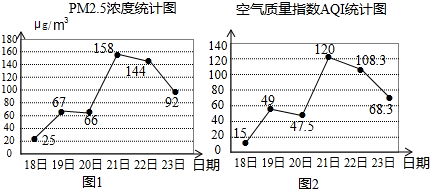
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
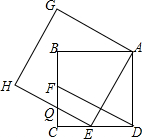 如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.
如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com