
【题目】若一次函数y=kx+m的图象经过二次函数y=ax2+bx+c的顶点,我们则称这两个函数为“丘比特函数组”
(1)请判断一次函数y=﹣3x+5和二次函数y=x2﹣4x+5是否为“丘比特函数组”,并说明理由.
(2)若一次函数y=x+2和二次函数y=ax2+bx+c为“丘比特函数组”,已知二次函数y=ax2+bx+c顶点在二次函数y=2x2﹣3x﹣4图象上并且二次函数y=ax2+bx+c经过一次函数y=x+2与y轴的交点,求二次函数y=ax2+bx+c的解析式;
(3)当﹣3≤x≤﹣1时,二次函数y=x2﹣2x﹣4的最小值为a,若“丘比特函数组”中的一次函数y=2x+3和二次函数y=ax2+bx+c(b、c为参数)相交于PQ两点请问PQ的长度为定值吗?若是,请求出该定值;若不是,请说明理由.
【答案】(1)不是,见解析;(2)抛物线的表达式为:y=﹣![]() x2+2x+2或y=x2+2x+2;(3)2
x2+2x+2或y=x2+2x+2;(3)2![]() ,为定值,见解析
,为定值,见解析
【解析】
(1)y=x2-4x+5=(x-2)2+1,即顶点坐标为(2,1),当x=2时,y=-3x+5=-1≠1,即可求解;
(2)根据题意可设顶点坐标为(m,m+2),将顶点坐标代入二次函数y=2x2-3x-4得:m+2=2m2-3m-4,解得:m=3或-1,即可求解;
(3)根据函数与x轴交点判断出:当-3≤x≤-1时,函数在x=-1时取得最小值,即a=1+2-4=-1,设抛物线的顶点为P(m,2m+3), “丘比特函数组”另外一个交点为Q(x,2x+3),则抛物线的表达式为:y=a(x-m)2+(2m+3)=-(x-m)2+(2m+3),把Q代入得:-(x-m)2+(2m+3)=2x+3,进行整理,再由韦达定理得:x+m=2m-2,解得:x=m-2,故点Q(m-2,2m-1),即可求解.
解:(1)y=x2﹣4x+5=(x﹣2)2+1,即顶点坐标为(2,1),
当x=2时,y=﹣3x+5=-1≠1,
故一次函数y=﹣3x+5和二次函数y=x2﹣4x+5不是“丘比特函数组”;
(2)设二次函数的顶点为:(m,m+2),
将顶点坐标代入二次函数y=2x2﹣3x﹣4得:m+2=2m2﹣3m﹣4,
解得:m=3或﹣1,
当m=3时,函数顶点为(3,5), 则二次函数表达式为:y=a(x﹣3)2+5,
又∵一次函数y=x+2与y轴的交点为:(0,2),
∴把(0,2)代入得:9a+5=2,解得:a=![]() ,
,
故抛物线的表达式为:y=![]() x2+2x+2;
x2+2x+2;
同理当m=﹣1时,抛物线的表达式为:y=x2+2x+2,
综上,抛物线的表达式为:y=![]() x2+2x+2或y=x2+2x+2;
x2+2x+2或y=x2+2x+2;
(3)是定值,理由:
令y=x2﹣2x﹣4=0,则x=1±![]() ,
,
故当﹣3≤x≤﹣1时,函数在x=﹣1时取得最小值,
即a=1+2﹣4=﹣1,
设抛物线的顶点为P(m,2m+3), “丘比特函数组”另外一个交点为Q(x,2x+3),
则抛物线的表达式为:y=a(x﹣m)2+(2m+3)=﹣(x﹣m)2+(2m+3),
把Q代入得:﹣(x﹣m)2+(2m+3)=2x+3,
整理得:x2+(2﹣2m)x+(m2﹣2m)=0,
由韦达定理得:x+m=2m﹣2,解得:x=m﹣2,故点Q(m﹣2,2m﹣1),
则PQ=![]() =2
=2![]() ,为定值.
,为定值.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形OABC的顶点O在坐标原点,顶点A,C在反比例函数y=![]() 的图象上,点A的横坐标为4,点B的横坐标为6,且平行四边形OABC的面积为9,则k的值为_____.
的图象上,点A的横坐标为4,点B的横坐标为6,且平行四边形OABC的面积为9,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
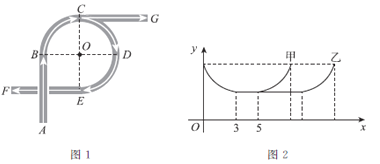
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计), A为入口, F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF ;弯道为以点O为圆心的一段弧,且![]() ,
,![]() ,
,![]() 所对的圆心角
所对的圆心角![]() 均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法:①甲车在立交桥上共行驶8s;②从F口出比从G口出多行驶40m;③甲车从F口出,乙车从G口出;④立交桥总长为150m.其中正确的是( )
均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法:①甲车在立交桥上共行驶8s;②从F口出比从G口出多行驶40m;③甲车从F口出,乙车从G口出;④立交桥总长为150m.其中正确的是( )
A. ①②③ B. ①②④ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)试确定该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
(2)试确定抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD![]() DE于点D, CE
DE于点D, CE![]() DE 于点 E.
DE 于点 E.
(1)若BC在DE的同侧(如图所示),且AD=CE,求证:![]()
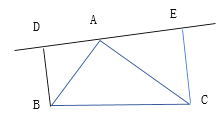
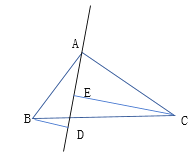
(2)若B、C在的两侧(如图所示 ),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
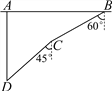
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
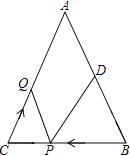
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 点向
点向![]() 点运动,设运动时间为
点运动,设运动时间为![]() (秒)
(秒)![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长度;
的长度;
(2)若点![]() 、
、![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 、
、![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度
的运动速度![]() 为多少时,能够使
为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE是直角梯形ABCD的高,将△ADE沿DE翻折,腰AD恰好经过腰BC的中点,则AE:BE等于( )
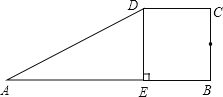
A.2:1 B.1:2 C.3:2 D.2:3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com