
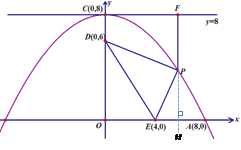
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

【答案】(1)抛物线的解析式为y=﹣![]() x2+8;(2)PD与PF的差是定值,PD﹣PF=2;(3)①P(4,6),此时△PDE的周长最小;②共有11个令S△DPE为整数的点.
x2+8;(2)PD与PF的差是定值,PD﹣PF=2;(3)①P(4,6),此时△PDE的周长最小;②共有11个令S△DPE为整数的点.
【解析】(1)设抛物线的解析式为y=a(x+h)2+k
∵点C(0,8)是它的顶点坐标, ∴y=ax2+8
又∵经过点A(8,0),
有64a+8=0,解得a=![]()
故抛物线的解析式为:y=![]() x2+8;
x2+8;
(2)是定值,解答如下:
设P(a,![]() a2+8),则F(a,8),
a2+8),则F(a,8),
∵D(0,6),
∴PD=![]()
PF=![]() ,
,
∴PD﹣PF=2;
(3)当点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小,
∵PD﹣PF=2,∴PD=PF+2,
 ∴PE+PD=PE+PF+2,
∴PE+PD=PE+PF+2,
∴当P、E、F三点共线时,PE+PF最小,
此时点P,E的横坐标都为4,
将x=4代入y=![]() x2+8,得y=6,
x2+8,得y=6,
∴P(4,6),此时△PDE的周长最小.
过点P做PH⊥x轴,垂足为H.
设P(a,![]() a2+8)
a2+8)
∴PH=![]() a2+8,EH=a-4,OH=a
a2+8,EH=a-4,OH=a
S△DPE=S梯形PHOD-S△PHE-S△DOE
=![]()
=![]()
=![]()
∵点P是抛物线上点A,C间的一个动点(含端点)
∴0≤a≤8
当a=6时,S△DPE取最大值为13.
当a=0时,S△DPE取最小值为4.
即4≤S△DPE≤13
其中,当S△DPE=12时,有两个点P.
所以,共有11个令S△DPE为整数的点.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】一个三角形中,有一个角是55°,另外的两个角可能是( )
A. 95°,20° B. 45°,80° C. 55°,60° D. 90°,20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年4月21日在深圳体育馆召开的第八届中国(深圳)国际茶业文化博览会上某茶商将甲、乙两种茶叶卖出,甲种茶叶卖出1200元,盈利20%,乙种茶叶卖出1200元,亏损20%,则此人在这次交易中是( )
A.盈利50元
B.盈利100元
C.亏损150元
D.亏损100元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,-3),顶点坐标为(-1,-4),
(1)求这个二次函数的解析式;
(2)求图象与x轴交点A、B两点的坐标;
(3)图象与y轴交点为点C,求三角形ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com