
 如图,已知抛物线y=ax2+bx+c经过A(-2,-2),B(3,3),C(0,6).
如图,已知抛物线y=ax2+bx+c经过A(-2,-2),B(3,3),C(0,6).分析 (1)由抛物线过A、B、C三点,利用待定系数法即可求出结论;
(2)由同底的三角形面积相等可知两三角形高相等,求出直线AC的解析式,由点到直线的距离即可找出P点的坐标;
(3)设出Q点坐标,由两点间的距离公式结合勾股定理即可得出结论.
解答 解:(1)∵抛物线y=ax2+bx+c经过A(-2,-2),B(3,3),C(0,6),
∴有$\left\{\begin{array}{l}{-2=4a-2b+c}\\{3=9a+3b+c}\\{6=c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=6}\end{array}\right.$.
故该抛物线的解析式为y=-x2+2x+6.
(2)∵抛物线的解析式为y=-x2+2x+6,
∴抛物线的对称轴为x=-$\frac{2}{2×(-1)}$=1.
假设存在符合题意的点P,设P点坐标为(1,m),直线AC的解析式为y=kx+b.
由点A(-2,-2),点C(0,6)在直线AC上可知,
$\left\{\begin{array}{l}{-2=-2k+b}\\{6=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=4}\\{b=6}\end{array}\right.$.
故直线AC的解析式为4x-y+6=0.
∵△APC与△ABC的面积相等,
∴点B、点P到直线AC的距离相等,
即$\frac{|4×3-3+6|}{\sqrt{{4}^{2}+(-1)^{2}}}$=$\frac{|4-m+6|}{\sqrt{{4}^{2}+(-1)^{2}}}$,
解得:m=-5,或m=20.
故抛物线对称轴上存在点P,使△APC与△ABC的面积相等,点P的坐标为(1,-5)或(1,20).
(3)假设存在符合条件的点Q,设Q点的坐标为(1,n).
由两点间的距离公式可知:
AC2=[0-(-2)]2+[6-(-2)]2=68,AQ2=[1-(-2)]2+[n-(-2)]2=9+(n+2)2,CQ2=(1-0)2+(n-6)2=1+(n-6)2,
∵∠AQC=90°,
∴AC2=AQ2+CQ2,
即68=9+(n+2)2+1+(n-6)2,
解得:n=2±$\sqrt{13}$.
故抛物线对称轴上存在点Q,使∠AQC=90°,Q点坐标为(1,2+$\sqrt{13}$)或(1,2-$\sqrt{13}$).
点评 本题考查了待定系数法求解析式、点到直线的距离以及两点间的距离公式,解题的关键是:(1)利用待定系数法求解析式;(2)同底等高的三角形面积相等;(3)两点间的距离公式结合勾股定理得出关于n的一元二次方程.本题属于中档题,难度不大,(1)没有难度;(2)(3)需要用到点到直线的距离.解决该类型题目时,可以假设存在符合条件的点,设出点的坐标,利用已知条件将求坐标转化成求一元二次方程的根.


科目:初中数学 来源: 题型:选择题
| A. | 6.9×102 | B. | 6.9×103 | C. | 6.9×107 | D. | 6.9×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 函数图象经过点(0,0) | B. | 函数图象不经过第四象限 | ||
| C. | y随x的增大而减小 | D. | 不论x为何值,总有y>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
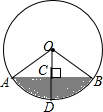 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com