
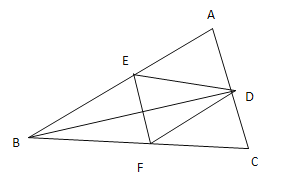
【题目】在△ABC中,AB=BC,点D在AC上,BD=6cm,E,F分别是AB,BC边上的动点,△DEF周长的最小值为6 cm,则![]() ( )
( )
A.20°B.25°C.30°D.35°
【答案】C
【解析】
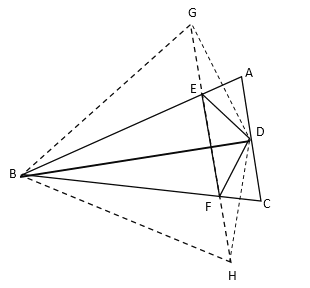
作点D关于AB的对称点G,关于BC的对称点H,连接GH交AB于E,交BC于F,连接BG、BH,此时△DEF的周长最小,根据轴对称关系得到BG=BD=BH=6cm,又由△DEF的周长=DE+DF+EF=GH=6cm,得到∠GBH=60°,由此即可求出∠ABC的度数.
作点D关于AB的对称点G,关于BC的对称点H,连接GH交AB于E,交BC于F,连接BG、BH,此时△DEF的周长最小,
由轴对称得:BG=BD=BH=6cm,∠GBA=∠DBA,∠HBC=∠DBC,
∵△DEF的周长=DE+DF+EF=GH=6cm,
∴△BGH是等边三角形,
∴∠GBH=60°,
∴∠ABC=![]() ∠GBH=30°,
∠GBH=30°,
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
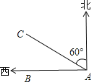
【题目】如图,某货船以![]() 海里/小时的速度将一批重要物资由
海里/小时的速度将一批重要物资由![]() 处运往正西方向的目的地
处运往正西方向的目的地![]() 处,经
处,经![]() 小时的航行到达,到达后必须立即卸货,接到气象部门的通知,一台风中心正以
小时的航行到达,到达后必须立即卸货,接到气象部门的通知,一台风中心正以![]() 海里/小时的速度由
海里/小时的速度由![]() 向北偏西
向北偏西![]() 方向移动,距台风中心
方向移动,距台风中心![]() 海里
海里
的圆形区域(包括边界)都会受到影响.
(1)![]() 处是否会受到台风的影响答:________(请填“会”或“不会”)
处是否会受到台风的影响答:________(请填“会”或“不会”)
![]() 为避免受到台风的影响,该船应在________小时内卸完货物.(结果保留根号)
为避免受到台风的影响,该船应在________小时内卸完货物.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
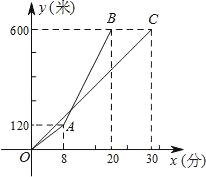
【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
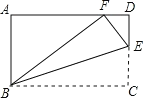
A. 2 B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
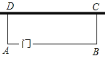
【题目】如图,现有![]() 长的篱笆,要围一个面积为
长的篱笆,要围一个面积为![]() 的花圃,花圃的一边靠墙(墙长
的花圃,花圃的一边靠墙(墙长![]() ),并在与墙平行的一边
),并在与墙平行的一边![]() 另外安装一道
另外安装一道![]() 宽的木门,那么花圃
宽的木门,那么花圃![]() 边的长为________
边的长为________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
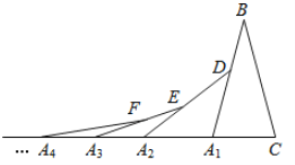
【题目】如图,在第1个![]() 中,
中,![]() ,
,![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第2个
,得到第2个![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .得到第3个
.得到第3个![]() ...按此做法继续下去,则第
...按此做法继续下去,则第![]() 个三角形中以
个三角形中以![]() 为顶点的内角度数是( )
为顶点的内角度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一老人坐在MN这层台阶上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问老人能否还晒到太阳?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com