
分析 在Rt△AEB中,根据勾股定理得到AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{1{2}^{2}+{8}^{2}}$=6$\sqrt{6}$,在Rt△AEC中,根据勾股定理得到AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15,在Rt△AED中,根据勾股定理得到AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{1{2}^{2}+1{0}^{2}}$=2$\sqrt{61}$,由于6$\sqrt{6}$+15+2$\sqrt{61}$<50,于是得到结果.
解答 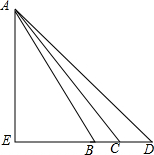 解:如图,在Rt△AEB中,∵AE=12,BE=8,
解:如图,在Rt△AEB中,∵AE=12,BE=8,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{1{2}^{2}+{8}^{2}}$=6$\sqrt{6}$,
在Rt△AEC中,∵AE=12,CE=9,
∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
在Rt△AED中,∵AE=12,DE=10,
∴AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{1{2}^{2}+1{0}^{2}}$=2$\sqrt{61}$,
∵6$\sqrt{6}$+15+2$\sqrt{61}$<50,
∴长为50米的铁索够用.
点评 本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.


科目:初中数学 来源: 题型:解答题
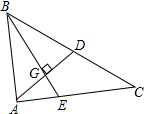 我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多“美妙”的性质.如关于线段比、面积比就有一些“漂亮”的结论,利用这些性质可以解决三角形的若干问题.请你利用重心的性质解决如下问题:
我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多“美妙”的性质.如关于线段比、面积比就有一些“漂亮”的结论,利用这些性质可以解决三角形的若干问题.请你利用重心的性质解决如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
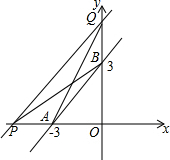 如图所示,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,3).一次函数图象与两坐标轴的交点P,Q在直线AB的同侧,且直线PQ与y轴交点在y轴正半轴上,若△QAB和△PAB的面积都等于3,求这个一次函数的解析式.
如图所示,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,3).一次函数图象与两坐标轴的交点P,Q在直线AB的同侧,且直线PQ与y轴交点在y轴正半轴上,若△QAB和△PAB的面积都等于3,求这个一次函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com