
【题目】如图,Rt△APE,∠AEP=90°,以AB为直径的⊙,O交PE于C,且AC平分∠EAP.连接BC,PB:PC=1:2.
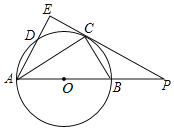
(1)求证:PE是⊙O的切线;
(2)已知⊙O的半径为![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)4
【解析】
(1)连接OC,由AC平分∠EAP,得到∠DAC=∠OAC,由等腰三角形的性质得到∠CAO=∠ACO,等量代换得到∠DAC=∠ACO,根据平行线的性质得到∠E=∠OCP=90°,于是得到结论;
(2)设PB=x,PC=2x,根据勾股定理得到PC=![]() ,
,![]() 求得AP=
求得AP=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
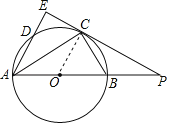
解:(1)连接OC,
∵AC平分∠EAP,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠DAC=∠ACO,
∴AE∥OC,
∴∠E=∠OCP=90°
∴PE是⊙O的切线;.
(2)∵PB:PC=1:2,
∴设PB=x,PC=2x,
∵OC2+PC2=OP2,即(![]() )2+(2x)2=(
)2+(2x)2=(![]() +x)2,
+x)2,
∴x=![]() ,.
,.
∴PC=![]() ,PB=
,PB=![]() ,
,
∴AP=![]() ,.
,.
∵OC∥AE,
∴△PCO∽△PEA,
∴![]()
∴AE=4.


科目:初中数学 来源: 题型:
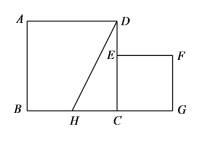
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
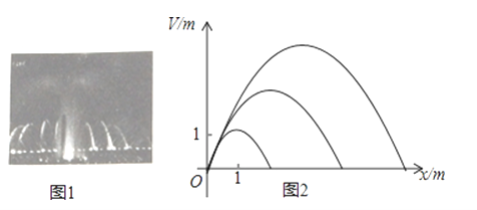
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的![]() ;
;
(2)问两动点经过多长时间使得点P与点Q之间的距离为![]() ?若存在,
?若存在,
求出运动所需的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
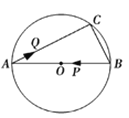
【题目】如图,AB是⊙O的直径,弦BC=6cm,AC=8cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁迅猛发展,给我们的出行带来极大的便捷,如图1,是某种新设计动车车头的纵截面一部分,曲线OBA是一开口向左,对称轴正好是水平线OC的抛物线的一部分,点A、B是车头玻璃罩的最高点和最低点,AC、BD是两点到车厢底部的距离,OD=1.5米,BD=1.5米,AC=3米,请你利用所学的函数知识解决以下问题.
(1)为了方便研究问题,需要把曲线OBA绕点O旋转转化为我们熟悉的函数,请你在所给的方框内,画出你旋转后函数图象的草图,在图中标出点O、A、B、C、D对应的位置,并求你所画的函数的解析式.
(2)如图2,驾驶员座椅安装在水平线OC上一点P处,实验表明:当PA+PB最小时,驾驶员驾驶时视野最佳,为了达到最佳视野,求OP的长.
(3)驾驶员头顶到玻璃罩的高度至少为0.3米才感到压抑,一个驾驶员坐下时头顶到椅面的距离为1米,在(2)的情况下,座椅最多条件到多少时他才感到舒适?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标
(3)已知点D(m,m+1)在第一象限的抛物线上,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com