
分析 ①△ABC是锐角三角形时,先根据高线的定义求出∠ADB=90°,∠BEC=90°,然后根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;
②△ABC是钝角三角形时,根据直角三角形两锐角互余求出∠BHC=∠A,从而得解.
解答 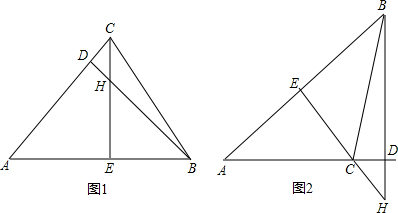 解:①如图1,△ABC是锐角三角形时,
解:①如图1,△ABC是锐角三角形时,
∵BD、CE是△ABC的高线,
∴∠ADB=90°,∠BEC=90°,
在△ABD中,∵∠A=65°,
∴∠ABD=90°-65°=25°,
∴∠BHC=∠ABD+∠BEC=25°+90°=115°;
②如图2,△ABC是钝角三角形时,
∵BD、CE是△ABC的高线,
∴∠A+∠ACE=90°,∠BHC+∠HCD=90°,
∵∠ACE=∠HCD(对顶角相等),
∴∠BHC=∠A=65°.
综上所述,∠BHC的度数是115°或65°.
点评 本题主要考查了三角形的内角和定理,三角形的高线,难点在于要分△ABC是锐角三角形与钝角三角形两种情况讨论,作出图形更形象直观.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
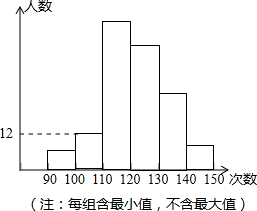 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
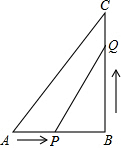 如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:
如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
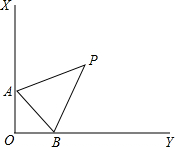 如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.
如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com