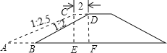
【题目】为了落实“三个代表”重要思想，确保人民群众利益，抵御百年不遇的洪水，市政府决定今年将
米长的粑铺大堤的迎水坡面铺石加固．如图，堤高
米，堤面加宽
米，坡度由原来的
改成
．则完成这一工程需要的石方数为________立方米．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】从如图所示的二次函数
（
）的图象中，观察得出了下面5条信息：①
；②
；③
；④
；⑤
.你认为其中正确的信息有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
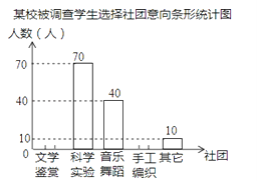
【题目】为了深化改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：
某校被调查学生选择社团意向统计表
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息，解答下列问题：
（1）求本次调查的学生总人数及a，b，c的值；
（2）将条形统计图补充完整；
（3）若该校共有1200名学生，试估计全校选择“科学实验”社团的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB＝16，O为AB中点，点C在线段OB上（不与点O，B重合），将OC绕点O逆时针旋转270°后得到扇形COD，AP，BQ分别切优弧
于点P，Q，且点P， Q在AB异侧，连接OP．
（1）求证：AP＝BQ；
（2）当BQ＝4
时，求扇形COQ的面积及
的长（结果保留π）；
（3）若△APO的外心在扇形COD的内部，请直接写出OC的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
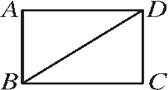
【题目】如图，BD是矩形ABCD的一条对角线．
(1)作BD的垂直平分线EF，分别交AD，BC于点E，F，垂足为点O；(要求用尺规作图，保留作图痕迹，不要求写作法)
(2)在(1)中，连接BE和DF，求证：四边形DEBF是菱形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=﹣2x2+4x与x轴的另一个交点为A，现将抛物线向右平移m（m＞2）个单位长度，所得抛物线与x轴交于C，D，与原抛物线交于点P，设△PCD的面积为S，则用m表示S正确的是（ ）
A. 
（m2﹣4） B. 
m2﹣2 C. （4﹣m2） D. 2﹣m2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y1=﹣x+4，y2=
x+b都与双曲线y=
交于点A（1，m），这两条直线分别与x轴交于B，C两点．
（1）求y与x之间的函数关系式；
（2）直接写出当x＞0时，不等式x+b＞的解集；
（3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形 ABCD 中，对角线 AC、BD 相交于点 O，过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H．
（感知）如图①，若四边形 ABCD 是正方形，且 AG＝BE＝CH＝DF，则 S 四边形AEOG＝ S 正方形 ABCD；
（拓展）如图②，若四边形 ABCD 是矩形，且 S 四边形 AEOG＝
S 矩形 ABCD，设 AB＝a， AD＝b，BE＝m，求 AG 的长（用含 a、b、m 的代数式表示）；
（探究）如图③，若四边形 ABCD 是平行四边形，且 AB＝3，AD＝5，BE＝1， 试确定 F、G、H 的位置，使直线 EF、GH 把四边形 ABCD 的面积四等分．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ABC=90°，CD⊥BC，BD与AC相交于点E，AB=9，BC=4，DC=3．
（1）求BE的长度；
（2）求△ABE的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
