
【题目】(1)请你根据下面画图要求,在图①中完成画图操作并填空.
如图①,△ABC中,∠BAC=30°,∠ACB=90°,∠PAM=∠A.
操作:(1)延长BC.
(2)将∠PAM绕点A逆时针方向旋转60°后,射线AM交BC的延长线于点D.
(3)过点D作DQ∥AB.
(4)∠PAM旋转后,射线AP交DQ于点G.
(5)连结BG.
结论:![]() = .
= .
(2)如图②,△ABC中,AB=AC=1,∠BAC=36°,进行如下操作:将△ABC绕点A按逆时针方向旋转α度角,并使各边长变为原来的n倍(n>1),得到△AB′C′.当点B、C、B′在同一条直线上,且四边形ABB′C′为平行四边形时(如图③),求a和n的值.

【答案】(1)![]() ;(2)72°;2.62.
;(2)72°;2.62.
【解析】
试题分析:(1)根据旋转得出△ABC~△AGD,设AB为2,根据30°的直角三角形的性质得出AD=2![]() ,进一步得出AG=4,可得
,进一步得出AG=4,可得![]() ;
;
(2)由四边形ABB′C′是平行四边形,易求得a=36°,又由△ABC∽△AB′C′,根据相似三角形的对应边成比例,继而求得答案.
试题解析:(1)如图:
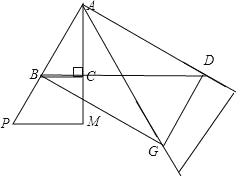
∵∠BAC=30°,∠ACB=90°,
∴∠PAM=∠A=30°,
∵∠PAM绕点A逆时针方向旋转60°,
∴∠BAG=60°,△ABC~△AGD,
∴∠GAD=∠BAC=∠MAG=30°,
∴△BAD是Rt△,∠ABD=60°,
∴∠ADB=30°,
设AB为2,则可得AD=![]() ,
,
∵DQ∥AB,∠BAD=90°
∴∠ADG=90°,
∵∠GAD=30°,AD=![]() ,
,
∴AG=4,
∴![]() ;
;
(2)∵四边形ABB′C′是平行四边形,
∴AC′∥BB′,
又∵∠BAC=36°,AB=AC
∴∠ABC=72°.
∴∠B′AC′=∠BAC=36°,
∴∠CAB′=36°,
∴α=180°-72°-36°=72°;
∴∠B′AC′=∠BAC=36°,而∠B=∠AB′C′,
∴△ABC∽△AB′C′,
∴AB:BB′=CB:AB,
∴AB2=CBAB′,
而 AB=1,
BC=2ABsin18°≈0.618,
所以可得n=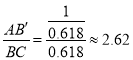 .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+2x-1=0有两个不相等的实数根,则m的取值范围是( ).
A. m>-1且m≠0 B. m<1且m≠0 C. m<-1 D. m>1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在创建绿色和谐校园活动中要在一块三角形花圃里种植两种不同的花草,同时拟从A点修建一条花间小径到边BC。
(1)若要使修建小路所使用的材料最少,请在图中画出小路AD,你的理由是 。
(2) 将如图方格中的图形向右平移4格,再向上平移2格,在方格中画出平移后的图形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),B(0,4![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com