
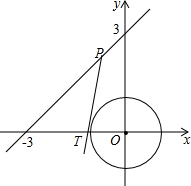
 如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.
如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$. 分析 由PT=$\sqrt{P{O}^{2}-O{T}^{2}}$可知求出OP的最小值即可解决问题.
解答 解:∵PT是切线,
∴PT⊥OT,
∴∠PTO=90°,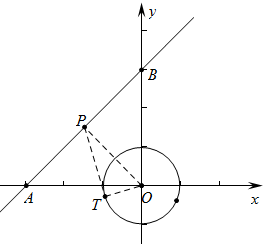
∴PT=$\sqrt{P{O}^{2}-O{T}^{2}}$,
要求PT最小值只要求OP的最小值,如图作OP⊥AB垂足为P,此时OP最小,
∵OA=OB=3,
∴点P坐标(-$\frac{3}{2}$,$\frac{3}{2}$),OP=$\frac{3\sqrt{2}}{2}$,
∴PT=$\sqrt{P{O}^{2}-O{T}^{2}}$=$\sqrt{\frac{18}{4}-1}$=$\frac{\sqrt{14}}{2}$.
故答案为$\frac{{\sqrt{14}}}{2}$
点评 本题考查切线的性质、一次函数的有关知识、垂线段最短、勾股定理等知识,解题的关键是PT=$\sqrt{P{O}^{2}-O{T}^{2}}$,要求PT最小值只要求OP的最小值,学会转化的思想,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图是一个平面直角坐标系,在坐标系中描出下列各点:A(1,2),B(3,2),C(-1,1),D(-1,-2).
如图是一个平面直角坐标系,在坐标系中描出下列各点:A(1,2),B(3,2),C(-1,1),D(-1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系xOy中,已知点B(0,2),点A在x轴正半轴上且∠BAO=30°.将△OAB沿直线AB折叠得△CAB,则点C的坐标为( )
在平面直角坐标系xOy中,已知点B(0,2),点A在x轴正半轴上且∠BAO=30°.将△OAB沿直线AB折叠得△CAB,则点C的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,3) | C. | (3,$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )
如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com