
����Ŀ��������C1��y1=mx2��4mx+2n��1��ƽ����x���ֱ�߽���A��B���㣬��A������Ϊ����1��2��������ͼ��������½��ۣ��ٶԳ���Ϊֱ��x=2������������y�ύ������Ϊ��0����1������m��![]() ������������C2��y2=ax2��a��0�����߶�ABǡ��һ�������㣬��a��ȡֵ��Χ��
������������C2��y2=ax2��a��0�����߶�ABǡ��һ�������㣬��a��ȡֵ��Χ��![]() ��a��2���ݲ���ʽmx2��4mx+2n��0�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ������������ȷ���۵ĸ����У� ��
��a��2���ݲ���ʽmx2��4mx+2n��0�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ������������ȷ���۵ĸ����У� ��

A. 2�� B. 3�� C. 4�� D. 5��
���𰸡�B
��������
���������ߵĶԳ���ֱ�߹�ʽ��������öԳ���ֱ�ߣ�������������������Ľ���������ص㣬�ó�C�������Ϊ����0��2n-1��;��A�����꣨-1.2�����������߽���ʽ��������:2n=3-5m,�ٴ���![]() �������ã�
�������ã�![]()
����֪��������x�����������㣬��������б�ʽӦ�ô���0���Ӷ��г�����m�IJ���ʽ�����m��ȡֵ��Χ���������ߵĶԳ��ԣ�B�������ΪB��5��2������![]() ��ͼ��ֱ����A��Bʱ�������߶ηֱ�����ֻ��һ�������㣬��ʱ��a��ֵ�ֱ�Ϊ
��ͼ��ֱ����A��Bʱ�������߶ηֱ�����ֻ��һ�������㣬��ʱ��a��ֵ�ֱ�Ϊ![]() ,�Ӷ��ó�a��ȡֵ��Χ������ʽ
,�Ӷ��ó�a��ȡֵ��Χ������ʽ![]() �Ľ���Կ����ǣ�������
�Ľ���Կ����ǣ�������![]() λ��ֱ��y=-1�Ϸ��IJ��֣����ʱx��ȡֵ��Χ������
λ��ֱ��y=-1�Ϸ��IJ��֣����ʱx��ȡֵ��Χ������![]() ����ֵ��Χ֮�ڣ�Ȼ�������жϼ���.
����ֵ��Χ֮�ڣ�Ȼ�������жϼ���.
�������ߵĶԳ���Ϊֱ��![]() ��������ȷ��
��������ȷ��
�ڵ�x=0ʱ��y=2n-1,�ʢڴ���
�� ��A�����꣨-1.2�����������߽���ʽ��������:2n=3-5m
�ٴ���![]() �������ã�
�������ã�![]()
����֪��������x�����������㣬��
![]() ��������:
��������:![]()
��ã�m>![]() ����������.
����������.
���������ߵĶԳ��ԣ�B�������ΪB��5��2��
�����߶ηֱ�����ֻ��һ��������
��ʱ��a��ֵ�ֱ�Ϊ![]()
�ó�a��ȡֵ��Χ,��![]() ���ʢ���ȷ.
���ʢ���ȷ.
�ݲ���ʽ![]() �Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ����,�ʢ���ȷ,��ѡB.
�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ����,�ʢ���ȷ,��ѡB.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊ4������A��C�ֱ���x�ᡢy����������ϣ�������y����![]() x2��bx��c������B��C���㣬��DΪ�����ߵĶ��㣬����AC��BD��CD.
x2��bx��c������B��C���㣬��DΪ�����ߵĶ��㣬����AC��BD��CD.
(1)��������ߵĽ���ʽ��
(2)��������߶���D��������ı���ABDC�������
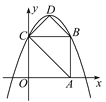
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�����������Сѧ����ʫ�ʴ������ijУ���꼶������ѧ��������Ԥѡ�����а���ǰ5��ѧ���ijɼ����ٷ��ƣ��ֱ�Ϊ���ˣ�1����86��85��77��92��85���ˣ�2����79��85��92��85��89��ͨ�����ݷ������б����£�
�༶ | ƽ���� | ��λ�� | ���� | ���� |
�ˣ�1�� | 85 | b | c | 22.8 |
�ˣ�2�� | a | 85 | 85 | 19.2 |
��1��ֱ��д������a��b��c��ֵ��
��2�������������ݷ���������Ϊ�ĸ���ǰ5��ͬѧ�ijɼ��Ϻã�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������żܿ��Խ��ƿ������ɵ�������ABD8D1�����Ϸ���������D1OD8���.��������ͼ��ʾ��ֱ������ϵ�����AB=44�ף���A=45�㣬AC1=4�ף���D2������Ϊ(-13��-1.69)�����żܵĹ���OH=________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ǽ�����һ�ǵ�ƽ���߶�Ӧ��ȵ�����������ȫ������_____���⣮��������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O������O���߶�EF��һ��Ա�AB��CD�ֱ��ཻ�ڵ�E��F��
��1����֤��AE=CF��
��2����AB=2����E��AB�е㣬��EF�ij���
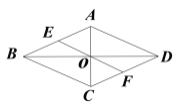
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��1�������������ϲ���Ŀ�����Ŀ����ȫ��ѧ�����е��飨ÿ��ѧ���ֱ�ѡһ�����Ŀ���������ݵ������г�ͳ�Ʊ������Ƴ�����ͳ��ͼ��

����������Ϣ����������⣺
��1��![]() ��
��![]() ��
��
��2������ͳ��ͼ�л�������Ŀ����Ӧ���ε�Բ�ĽǶ���Ϊ ![]() ��
��
��3����ѡ��ģ��Ŀ��![]() ��ѧ�������ѡȡ
��ѧ�������ѡȡ![]() ��ѧ���μ�ѧУ��ģ��ȤС��ѵ���������оٷ�������״ͼ���б�������ѡȡ��
��ѧ���μ�ѧУ��ģ��ȤС��ѵ���������оٷ�������״ͼ���б�������ѡȡ��![]() ��ѧ����ǡ����
��ѧ����ǡ����![]() ��������
��������![]() ��Ů���ĸ��ʣ�
��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����PΪ��ABC����ƽ����һ�㣬����APB=��BPC=��CPA=120�㣬���P������ABC�ķ����㣮
��1�������PΪ�����ABC�ķ����㣬����ABC=60�㣮
����֤����ABP�ס�BCP��
����PA=3��PC=4����PB= ��
��2����֪�����ABC���ֱ���AB��ACΪ������������ABE������ACD��CE��BD �ཻ��P�㣮��ͼ��2��
������CPD�Ķ�����
����֤��P��Ϊ��ABC�ķ����㣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com