
【题目】如图,AB是⊙O的直径,直线EF切⊙O于点C, AD⊥EF于点D.
(1)求证:AC平分∠BAD;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.(结果保留π)
【答案】
(1)证明:连接OC, ![]() 直线EF切
直线EF切 ![]() 于点C,
于点C, ![]()
![]()
![]()
![]()
![]()
![]()
![]() 即
即 ![]() 平分
平分 ![]() ;
;
(2)解: ![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形, ![]() 的半径为2,
的半径为2, ![]()
![]() 在
在 ![]() 中,
中, ![]() 由勾股定理得
由勾股定理得 ![]()
![]()
![]()
【解析】(1)抓住已知直线EF切⊙O于点C,因此连接OC,得出O C ⊥ E F , 根据 AD⊥EF,易得到OC∥AD,得出∠OCA=∠DAC,再根据同圆的半径相等及等量代换,易证得结论。
(2)观察图形可知S阴影=S梯形OCDAS扇形OCA,根据已知求出∠AOC的度数、AD、CD的长,即可求得结果。
【考点精析】关于本题考查的平行线的判定与性质和切线的性质定理,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图所示的函数图象反映的过程是:李大爷每天早上都到公园锻炼,他从家去公园锻炼一会儿,又去了菜市场后马上回家,其中![]() 表示时间,
表示时间,![]() 表示李大爷离他家的距离。
表示李大爷离他家的距离。
(1)李大爷家到公园的距离是多少千米,他在公园银炼了多少小时;
(2)李大爷从菜市场回家的平均速度;
(3)李大爷从家到菜市场的平均速度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.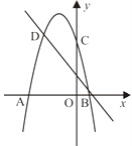
(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是( )
A.k> ![]()
B.k≥ ![]()
C.k> ![]() 且k≠1
且k≠1
D.k≥ ![]() 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x(秒),△PBQ的面只为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com