
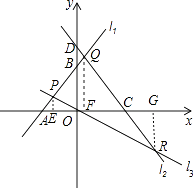
【题目】如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣ ![]() x交于点P.直线l3:y=﹣
x交于点P.直线l3:y=﹣ ![]() x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R. 
(1)点A的坐标是 , 点B的坐标是 , 点P的坐标是;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
【答案】
(1)(﹣3,0);(0,3);(﹣2,1)
(2)解:点P在直线l3上
∵P(﹣2,1),且将△POB沿y轴折叠后,点P与点P关于y轴对称,
∴P(2,1),
当x=2时,代入y=﹣ ![]() x+4得y=﹣
x+4得y=﹣ ![]() ×2+4=1,
×2+4=1,
∴点P在直线l3上
(3)解:分别过点P作PE⊥x轴于F,过点Q作QF⊥x轴于F,过点R作RG⊥x轴于G,
由 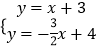 得
得 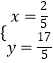 ,
,
∴Q( ![]() ,
, ![]() ),
),
由 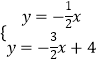 得
得 ![]()
∴R(4,﹣2),
对于y=﹣ ![]() x+4,则y=0得x=
x+4,则y=0得x= ![]() ,
,
∴C( ![]() ,0),
,0),
∴S△AQC= ![]() AC×QF=
AC×QF= ![]() ×(
×( ![]() +3)×
+3)× ![]() =
= ![]() ,S△OCR=
,S△OCR= ![]() OCGR=
OCGR= ![]() ×
× ![]() ×2=
×2= ![]() ,S△AOP=
,S△AOP= ![]() OAPE=
OAPE= ![]() ×3×1=
×3×1= ![]() ,
,
∴S△PQR=S△AQC+S△OCR﹣S△AOP= ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】解:(1)∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴令y=0,求得x=﹣3,令x=0,求得y=3,
∴A(﹣3,0)、B(0,3),
∵直线l1与直线l2y=﹣ ![]() x交于点P.
x交于点P.
∴解 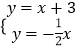 得
得 ![]() ,
,
∴P(﹣2,1),
所以答案是:(﹣3,0),(0,3),(﹣2,1);


科目:初中数学 来源: 题型:
【题目】若△ABC三边分别是a、b、c,且满足(b﹣c)(a2+b2)=bc2﹣c3, 则△ABC是( )
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D. 等腰或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
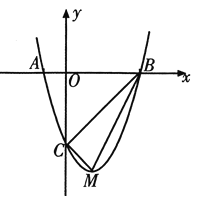
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com