
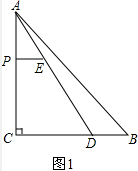
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围. 分析 先利用勾股定理求出AD,由PE∥CD得$\frac{AE}{AD}$=$\frac{AP}{AC}$,求出AE即可解决问题.
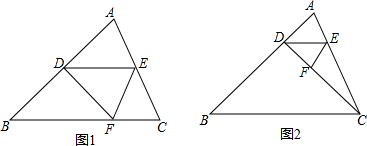
解答 解:如图1中, 在RT△ACD中,∵∠C=90°,AC=4,CD=3,
在RT△ACD中,∵∠C=90°,AC=4,CD=3,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵PE∥CD
∴$\frac{AE}{AD}$=$\frac{AP}{AC}$,
∴$\frac{AE}{5}$=$\frac{t}{4}$,
∴AE=$\frac{5t}{4}$,
∴DE=AD-AE=-$\frac{5}{4}$t+5,
∴y=-$\frac{5}{4}$t+5,(0<t<4).
点评 本题考查动点问题的函数图象、平行线成比例定理、勾股定理等知识,解题的关键是利用平行线分线段成比例定理解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
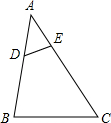 如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )
如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为21,那么AB的长为( )| A. | 5 | B. | 12.5 | C. | 25 | D. | $\sqrt{21}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
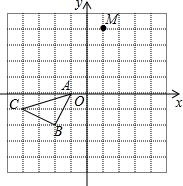 如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
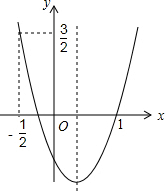 如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.
如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com