
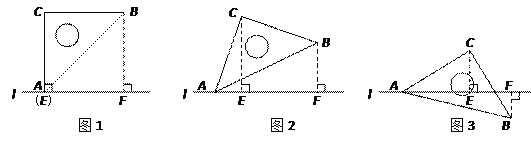
【题目】在平面内有一等腰直角三角板(∠ACB=90)和直线l.过点C作CE⊥l于点E,过点B作BF⊥l于点F.当点E与点A重合时(图①),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图②.图③的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,请直接写出线段AF.BF.CE之间的数量关系的猜想(不需证明).
【答案】见解析
【解析】分析:图2:过B作BH⊥CE于点H,易证△ACE≌△CBH.根据全等三角形的对应边相等,即可证得![]()
图3:过点C作CG⊥BF,交BF延长线于点G,易证△CBG≌△CAE,根据全等三角形的对应边相等,即可证得![]()
详解:图2,AF+BF=2CE仍成立,
证明:过B作BH⊥CE于点H,

∵∠BCH+∠ACE=90,
又∵在直角△ACE中,∠ACE+∠CAE=![]() ,
,
∴∠CAE=∠BCH,
又∵AC=BC,∠AEC=∠BHC=![]() ,
,
∴△ACE≌△CBH.
∴CH=AE,BF=HE,CE=BH,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
图3中,过点C作CG⊥BF,交BF延长线于点G,
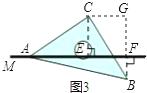
∵AC=BC,
可得∠AEC=∠CGB,
∠ACE=∠BCG,
∴△CBG≌△CAE,
∴AE=BG,
∵AF=AE+EF,
∴AF=BG+CE=BF+FG+CE=2CE+BF,
∴AFBF=2CE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )
(1)、![]() 的平方根是±5;(2)、五边形的内角和是540°;(3)、抛物线y=x2+2x+4与x轴无交点;(4)、等腰三角形两边长为6cm和4cm,则它的周长是16cm.
的平方根是±5;(2)、五边形的内角和是540°;(3)、抛物线y=x2+2x+4与x轴无交点;(4)、等腰三角形两边长为6cm和4cm,则它的周长是16cm.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
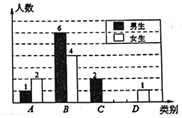
【题目】张老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)C类中女生有___名,D类中男生有___名,将下面条形统计图补充完整;
(2)若该校九年级共有女生180名,则九年级女生完成数学作业达到很好和较好的大约多少人?
(3)为了共同进步,张老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好性别相同的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点A的坐标为(0,1),点B的坐标为(3,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图1,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.

(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】未成年人思想道德建设越来越受到社会的关注.某青少年研究机构随机调查了某校 100名学生寒假花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查 数据制成了如下的频数分布表(部分空格未填).
某校 100 名学生寒假花零花钱数量的频数分布表:
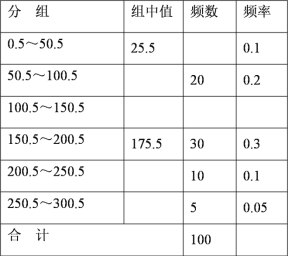
(1)完成该频数分布表;
(2)画出频数分布直方图.
(3)研究认为应对消费 150 元以上的学 生提出勤俭节约的建议.试估计应对该校1200 学生中约多少名学生提出该项建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班张山同学利用所学函数知识,对函数![]() 进行了如下研究:
进行了如下研究:
列表如下:
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:![]() ________,
________,![]() ________;
________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______.
的图象交点的坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com