
【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.

【答案】(1)详见解析;(2)![]()
【解析】
(1)由CP是⊙O的切线, AB是直径,得出∠BCD=∠BAC,∠ACB=90°,进而得到∠ACB=∠CDB=90°,即可得出结论;
(2)求出△OCB是正三角形,根据阴影部分的面积=S扇形OCB﹣S△OCB计算即可.
(1)如图,连接OC,

∵直线CP是⊙O的切线,∴∠BCD+∠OCB=90°,
∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°
∴∠BCD=∠ACO,
又∵OA=OC,∴∠BAC=∠ACO,∴∠BCD=∠BAC,
又∵BD⊥CP,
∴∠CDB=90°,∴∠ACB=∠CDB=90°,
∴△ACB∽△CDB;
(2)如图,连接OC,
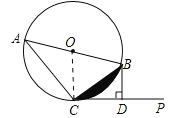
∵直线CP是⊙O的切线,∠BCP=30°,∴∠OCB=90°-∠BCP=60°.∵OC=OB,∴△OCB是正三角形.
∵⊙O的半径为1,∴S△OCB=![]() ,S扇形OCB=
,S扇形OCB=![]() =
=![]() π,
π,
故阴影部分的面积=S扇形OCB﹣S△OCB=![]() π﹣
π﹣![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A. B两种园艺造型共50个,摆放在迎宾大道两侧。已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆。
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,点E,F分别是BC,AD的中点,连接AE,CF.
(1)求证:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程是关于x的一元二次方程的是( )
A. ax2+bx+c=0 B. ![]() =2 C. x2+2x=y2-1 D. 3(x+1)2=2(x+1)
=2 C. x2+2x=y2-1 D. 3(x+1)2=2(x+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一次函数![]() 的图象与y轴交于点A,与反比例函数
的图象与y轴交于点A,与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
![]() ______;
______;![]() ______;
______;
![]() 点C是线段AB上的动点
点C是线段AB上的动点![]() 与点A、B不重合
与点A、B不重合![]() ,过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求
,过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求![]() 面积的最大值;
面积的最大值;
![]() 将
将![]() 中面积取得最大值的
中面积取得最大值的![]() 沿射线AB方向平移一定的距离,得到
沿射线AB方向平移一定的距离,得到![]() ,若点O的对应点
,若点O的对应点![]() 落在该反比例函数图象上
落在该反比例函数图象上![]() 如图
如图![]() ,则点
,则点![]() 的坐标是______.
的坐标是______.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com