
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,把
,把![]() 沿
沿![]() 轴对折,点
轴对折,点![]() 落到点
落到点![]() 处,过点
处,过点![]() 、
、![]() 的抛物线
的抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 、
、![]() .
.
(1)求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在直线![]() 上方的抛物线上求一点
上方的抛物线上求一点![]() ,使
,使![]() 面积最大,求出点
面积最大,求出点![]() 坐标;
坐标;
(3)在第一象限内的抛物线上,是否存在一点![]() ,作
,作![]() 垂直于
垂直于![]() 轴,垂足为点
轴,垂足为点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为项点的三角形与
为项点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)由直线![]() 可以求出A,B的坐标,由待定系数法就可以求出抛物线的解析式和直线BD的解析式;
可以求出A,B的坐标,由待定系数法就可以求出抛物线的解析式和直线BD的解析式;
(2)先求得点D的坐标,作EF∥y轴交直线BD于F,设![]() ,利用三角形面积公式求得
,利用三角形面积公式求得![]() ,再利用二次函数性质即可求得答案;
,再利用二次函数性质即可求得答案;
(3)如图1,2,分类讨论,当△BOC∽△MON或△BOC∽△ONM时,由相似三角形的性质就可以求出结论;
(1)∵直线AB为![]() ,
,
令y=0,则![]() ,令
,令![]() ,则y=2,
,则y=2,
∴点A、B的坐标分别是:A (-1,0),B(0,2),
根据对折的性质:点C的坐标是:(1,0) ,
设直线BD解析式为![]() ,
,
把B(0,2),C(1,0)代入![]() ,得
,得![]() ,
,
解得:![]() ,
,![]() ,
,
∴直线BD解析式为![]() ,
,
把A(-1,0),B(0,2)代入![]() 得
得![]() ,
,
解得:![]() ,
,![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)解方程组![]() 得:
得: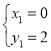 和
和 ,
,
∴点D坐标为(3,-4) ,
作EF∥y轴交直线BD于F
设![]()
∴![]()
![]() (0<
(0<![]() <3)
<3)
∴当![]() 时,三角形面积最大,
时,三角形面积最大,
此时,点![]() 的坐标为:
的坐标为:![]() ;
;
(3)存在.
∵点B、C的坐标分别是B (0,2)、C (1,0),
∴![]() ,
,![]() ,
,
①如图1所示,
当△MON∽△BCO时,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
将![]() 代入抛物线的解析式
代入抛物线的解析式![]() 得:
得:
![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴点M的坐标为(1,2);
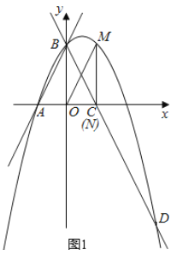
②如图2所示,
当△MON∽△CBO时,
∴![]() ,即
,即![]() ,
,
∴MN=![]() ON,
ON,
设![]() ,则M(b,
,则M(b,![]() b),
b),
将M(b,![]() b)代入抛物线的解析式
b)代入抛物线的解析式![]() 得:
得:
∴![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴点M的坐标为(![]() ,
,![]() ),
),
∴存在这样的点![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:已知![]() 是正方形
是正方形![]() 的对角线,将直角三角尺放在正方形
的对角线,将直角三角尺放在正方形![]() 上.
上.
(1)如图1,使三角尺的直角顶点与点![]() 重合,三角尺的一条直角边交直线
重合,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
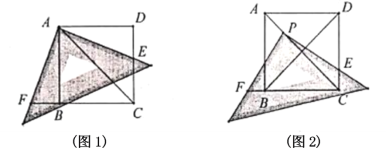
操作发现:
(2)如图2,将三角尺的直角项点![]() 放在
放在![]() 上,三角尺的一条直角边交直线
上,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若BA⊥AC,试判断四边形AFBD的形状,并证明你的结论.
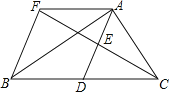
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
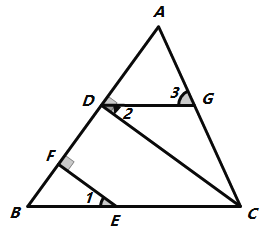
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: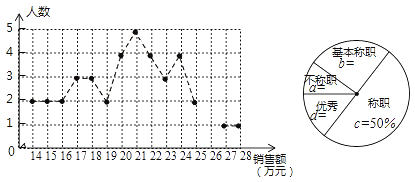
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.
(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个转盘被分成![]() 等分,每一份上各写有一个数字,随机转动转盘
等分,每一份上各写有一个数字,随机转动转盘![]() 次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,
次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,![]() 次转动后组成一个两位数(若指针停在等分线上则重新转一次)
次转动后组成一个两位数(若指针停在等分线上则重新转一次)
![]() 用画树状图的方法求出转动后所有可能出现的两位数的个数.
用画树状图的方法求出转动后所有可能出现的两位数的个数.
![]() 甲、乙两人做游戏,约定得到的两位数是偶数时甲胜,否则乙胜,这个游戏公平吗?请说明理由.
甲、乙两人做游戏,约定得到的两位数是偶数时甲胜,否则乙胜,这个游戏公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM,垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com