
【题目】综合与实践:
问题情境:已知![]() 是正方形
是正方形![]() 的对角线,将直角三角尺放在正方形
的对角线,将直角三角尺放在正方形![]() 上.
上.
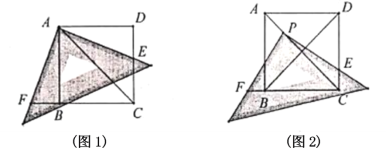
(1)如图1,使三角尺的直角顶点与点![]() 重合,三角尺的一条直角边交直线
重合,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
操作发现:
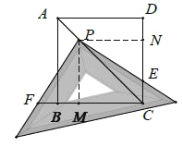
(2)如图2,将三角尺的直角项点![]() 放在
放在![]() 上,三角尺的一条直角边交直线
上,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)证明见解析(2)![]() ;详见解析
;详见解析
【解析】
(1)根据同角的余角相等,证明∠DAE=∠BAF,再根据ASA证明ΔAFB≌ΔAED,根据全等三角形对应边相等即可得出结论;
(2)过点P作PM⊥BC于点M,作PN⊥DC于点N,由正方形的性质得到∠PMC=∠PNC=∠MCN=90°,∠ACB=∠ACD,再由角平分线的性质和四边形内角和为360°得到∠MPN=90°,PM=PN,然后根据同角的余角相等,证明∠MPF=∠NPE,再根据ASA证明ΔPFMΔPEN,根据全等三角形对应边相等即可得出结论.
(1)证明:∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵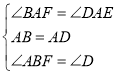
∴![]() (
(![]() )
)
∴![]() ;
;
(2)![]() .理由如下:
.理由如下:
过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,∠ABC=∠ACD,
,∠ABC=∠ACD,
∴![]() .
.
∵∠PMC+∠MCN+∠PNC+∠MPN=360°,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵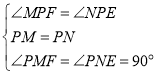 ,
,
∴![]() (
(![]() ),
),
∴![]() .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.
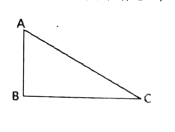
(1)作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ;(要求:不写作法,保留作图痕迹)
;(要求:不写作法,保留作图痕迹)
(2)判断(1)中![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(3)若![]() ,求出(1)中
,求出(1)中![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
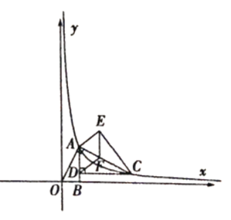
【题目】已知:如图,![]() 的顶点
的顶点![]() 是反比例函数
是反比例函数![]() 图象上一点,过点
图象上一点,过点![]() 作
作![]() 交反比例函数的图象于点
交反比例函数的图象于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
(1)求点![]() 的坐标;
的坐标;
(2)将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,连接
,连接![]() ,判断四边形
,判断四边形![]() 的形状并说明理由.
的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班要从甲乙两名同学中选派一人去参加学校举行的”扫黑除恶”知识竞赛,王老师准备用一副扑克牌中排列数字分别为![]() ,
,![]() ,
,![]() ,
,![]() 的四张扑克牌做抽数字游戏,决定谁去参加比赛,游戏规则为;将这四张牌的正面全部朝下,洗匀后从中随机抽取一张,得到的数字作为十位上的数字,然后将所抽到的牌放回,再从中随机抽取一张,得到的数字作为个位上的数字,这样就得到了一个两位数,若这个两位数小于
的四张扑克牌做抽数字游戏,决定谁去参加比赛,游戏规则为;将这四张牌的正面全部朝下,洗匀后从中随机抽取一张,得到的数字作为十位上的数字,然后将所抽到的牌放回,再从中随机抽取一张,得到的数字作为个位上的数字,这样就得到了一个两位数,若这个两位数小于![]() ,则甲胜,否则乙获胜,且游戏的获胜者将去参加比赛.
,则甲胜,否则乙获胜,且游戏的获胜者将去参加比赛.
(1)求抽取的扑克牌使得十位数字是![]() 的概率;
的概率;
(2)你认为这个游戏公平吗?请运用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
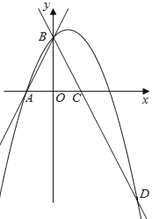
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,把
,把![]() 沿
沿![]() 轴对折,点
轴对折,点![]() 落到点
落到点![]() 处,过点
处,过点![]() 、
、![]() 的抛物线
的抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 、
、![]() .
.
(1)求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在直线![]() 上方的抛物线上求一点
上方的抛物线上求一点![]() ,使
,使![]() 面积最大,求出点
面积最大,求出点![]() 坐标;
坐标;
(3)在第一象限内的抛物线上,是否存在一点![]() ,作
,作![]() 垂直于
垂直于![]() 轴,垂足为点
轴,垂足为点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为项点的三角形与
为项点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com