
【题目】如图,在![]() 中,
中,![]() .
.
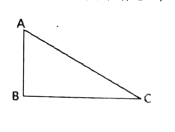
(1)作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ;(要求:不写作法,保留作图痕迹)
;(要求:不写作法,保留作图痕迹)
(2)判断(1)中![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(3)若![]() ,求出(1)中
,求出(1)中![]() 的半径.
的半径.
【答案】(1)答案见解析;(2)相切,理由见解析;(3)![]()
【解析】
(1)根据题意,尺规作角平分线,进而作圆,即可;
(2)过O点作OD⊥AC于D点,根据角平分线的性质定理,得OB=OD,进而即可得到结论;
(3)根据切线长定理得CD=CB=8,设OD=OB=x,根据勾股定理,列出方程,即可求解.
(1)如图所示;
(2)相切,理由如下:
过O点作OD⊥AC于D点,
∵CO平分∠ACB,∠ABC=90°,OD⊥AC,
∴OB=OD,即d=r,
∴⊙O与AC相切;
(3)∵Rt△ABC中,![]() ,
,
∴AC=10,
∵![]() ,即:AB⊥BC,
,即:AB⊥BC,
∵CB为⊙O的切线,
∴CD=CB=8,
∴AD=2,
设OD=OB=x,
由勾股定理得:22+x2=(6-x)2,解得:x=![]() ,
,
即:![]() 的半径为:
的半径为:![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=![]() ,点D为AC与反比例函数
,点D为AC与反比例函数![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
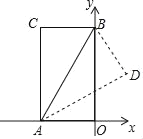
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
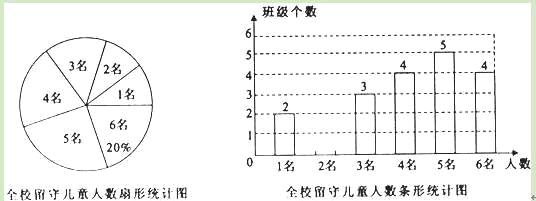
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:
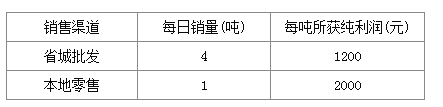
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:已知![]() 是正方形
是正方形![]() 的对角线,将直角三角尺放在正方形
的对角线,将直角三角尺放在正方形![]() 上.
上.
(1)如图1,使三角尺的直角顶点与点![]() 重合,三角尺的一条直角边交直线
重合,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
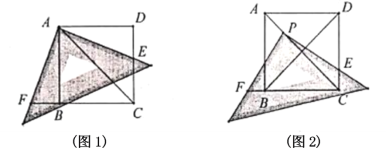
操作发现:
(2)如图2,将三角尺的直角项点![]() 放在
放在![]() 上,三角尺的一条直角边交直线
上,三角尺的一条直角边交直线![]() 于点
于点![]() ,另一条直角边交直线
,另一条直角边交直线![]() 于点
于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司以22元/千克的成本价购进1000kg苹果,公司想知道苹果的损坏率,随机抽取若干进行统计,部分结果如下表:
草果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.60 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
根据此表估计这批苹果损坏的概率(精确到0.1),从而计算该公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为_____元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
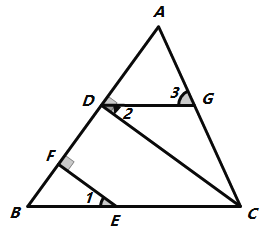
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com