
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
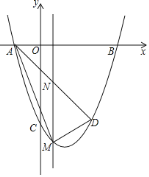
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的一点,当
是抛物线上的一点,当![]() 的面积是8,求出点
的面积是8,求出点![]() 的坐标;
的坐标;
(3)过直线![]() 下方的抛物线上一点
下方的抛物线上一点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,已知
,已知![]() 点的横坐标是
点的横坐标是![]() ,试用含
,试用含![]() 的式子表示
的式子表示![]() 的长及△ADM的面积
的长及△ADM的面积![]() ,并求当
,并求当![]() 的长最大时
的长最大时![]() 的值.
的值.
【答案】【解析】(1)y=(x-1)2-4, 点D的坐标为(2,-3);(2)点P的坐标为![]() 或
或![]() 或(1,-4);(3)当
或(1,-4);(3)当![]()
![]() ,
,![]() ,当MN的长最大时S的值为
,当MN的长最大时S的值为![]() .
.
【解析】
(1)根据点C的坐标,利用二次函数图象上点的坐标特征可求出n值,进而可得出抛物线的解析式,由抛物线的解析式利用二次函数的性质可得出抛物线的对称轴,结合点C的坐标可得出点D的坐标;
(2)利用二次函数图象上点的坐标特征可求出点A,B的坐标及AB的长,设点P的坐标为(a,b),由三角形的面积公式结合△ABP的面积是8,可求出b值,再利用二次函数图象上点的坐标特征可求出点P的坐标;
(3)根据点A,D的坐标利用待定系数法可求出直线AD的解析式,由点M的横坐标为m可得出点M,N的坐标,进而可得出MN的长,结合S=S△AMN+S△DMN可用含m的式子表示△ADM的面积S,再利用二次函数的性质即可解决最值问题.
解:(1)把C(0,-3)代入y=(x-1)2+n,得,-3=(0-1)2+n,
解得n=-4,∴抛物线的解析式为y=(x-1)2-4,
∴抛物线的对称轴为直线x=1∵点D与点C关于抛物线的对称轴对称,
∴点D的坐标为(2,-3).
(2)当y=0时,(x-1)2-4=0,
解得:x1=-1,x2=3,
∴点A的坐标为(-1,0),点B的坐标为(3,0),AB=3-(-1)=4.
设点P的坐标为(a,b),
∵△ABP的面积是8,
∴![]() AB|b|=8,即
AB|b|=8,即![]()
×4|b|=8,
∴b=±4.
当b=4时,(a-1)2-4=4,解得:a1=1-2![]() ,a2=1+2
,a2=1+2![]() ,
,
∴点P的坐标为(1-2![]() ,4)或(1+2
,4)或(1+2![]() ,4);
,4);
当b=-4时,(a-1)2-4=-4,解得:a3=a4=1,
∴点P的坐标为(1,-4).
∴当△ABP的面积是8,点P的坐标为(1-2![]() ,4)或(1+2
,4)或(1+2![]() ,4)或(1,-4).
,4)或(1,-4).
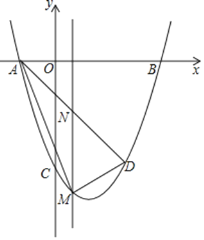
(3)设直线AD的解析式为y=kx+c(k≠0),
将A(-1,0),D(2,-3)代入y=kx+c,得:
![]() ,
,
解得:![]() ,
,
∴直线AD的解析式为y=-x-1.
∵点M的横坐标是m(-1<m<2),
∴点M的坐标为(m,(m-1)2-4),点N的坐标为(m,-m-1),
∴MN=-m-1-[(m-1)2-4]=-m2+m+2(-1<m<2),S=S△AMN+S△DMN=![]() MN(m+1)+
MN(m+1)+![]() MN(2-m)=
MN(2-m)=![]() mn=-
mn=-![]() m2+
m2+![]() m+3(-1<m<2).
m+3(-1<m<2).
∵MN=-m2+m+2=-(m-![]() )2+
)2+![]() ,-1<0,
,-1<0,
∴当m=![]() 时,MN取得最大值,最大值为
时,MN取得最大值,最大值为![]() ,此时S的值为
,此时S的值为![]() ×
×![]() =
=![]() ,
,
∴当MN的长最大时S的值为![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
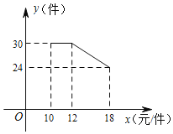
【题目】 某网店销售一种产品.这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/件市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示:
(1)当12≤x≤18时,求y与x之间的函数关系式;
(2)求每天的销售利润w(元)与销售价x(元/件)之间的函数关系式并求出每件销售价为多少元时.每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“特色福州,美好生活”,福州举行金色秋天旅游活动.明明和华华同学分析网上关于旅游活动的信息,发现最具特色的景点有:①鼓岭、②森林公园、③青云山.他们准备周日下午去参观游览,各自在这三中个景点任选一个,每个景点被选中的可能性相同.
(1)明明同学在三个备选景点中选中鼓岭的概率是 .
(2)用树状图或列表法求出明明和华华他们选中不同景点参观的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1) 若确定甲打第一场,再从其余三位同学中随机选取一位,恰好选中乙同学的概率是 .
(2) 若随机抽取两位同学,请用画树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市倡导垃圾分类投放,将日常垃圾分成四类,分别投放四种不同颜色的垃圾桶中,在“垃圾分类”模拟活动中,某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中,则这个同学正确分类投放垃圾的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校“综合实践”社团,计划利用![]() 长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为
长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为![]() .
.
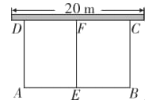
(1)能否围成总面积为![]() 的试验田?若能,求出
的试验田?若能,求出![]() 的长度;若不能,说明理由;
的长度;若不能,说明理由;
(2)能否围成总面积为![]() 的试验田?说说你的理由.
的试验田?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
阅读理解:数学兴趣小组在探究如何求![]() 的值,经过思考、讨论、交流,得到以下思路:
的值,经过思考、讨论、交流,得到以下思路:
如图1,作![]() ,使
,使![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.![]()
![]() .
.
请解决下列问题:
(1)类比求解:求出![]() 的值;
的值;
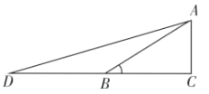
(2)问题解决:如图2,某住宅楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是
,当光线与地面的夹角是![]() 时,住宅在建筑物的墙上留下高
时,住宅在建筑物的墙上留下高![]() 的影子
的影子![]() ;而当光线与地面的夹角是
;而当光线与地面的夹角是![]() 时,住宅楼顶
时,住宅楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有
有![]() 的距离(
的距离(![]() ,
,![]() ,
,![]() 在一条直线上).求住宅楼
在一条直线上).求住宅楼![]() 的高度(结果保留根号);
的高度(结果保留根号);
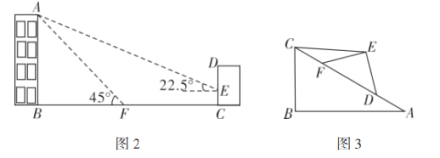
(3)探究发现:如图3,小明用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .他将
.他将![]() 的斜边
的斜边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() ,
,![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).探究在
重合).探究在![]() 移动过程中,是否存在某个位置,使得
移动过程中,是否存在某个位置,使得![]() ?如果存在,直接写出
?如果存在,直接写出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com