
【题目】为测量某特种车辆的性能,研究制定了行驶指数![]() ,而
,而![]() 的大小与平均速度
的大小与平均速度![]() 和行驶路程
和行驶路程![]() 有关(不考虑其他因素),
有关(不考虑其他因素),![]() 由两部分的和组成,一部分与
由两部分的和组成,一部分与![]() 成正比,另一部分与
成正比,另一部分与![]() 成正比.在实验中得到了表格中的数据:
成正比.在实验中得到了表格中的数据:
速度 |
|
|
路程 |
|
|
指数 |
|
|
(1)用含![]() 和
和![]() 的式子表示
的式子表示![]() ;
;
(2)当行驶指数为![]() ,而行驶路程为
,而行驶路程为![]() 时,求平均速度的值;
时,求平均速度的值;
(3)当行驶路程为![]() 时,若行驶指数值最大,求平均速度的值.
时,若行驶指数值最大,求平均速度的值.
【答案】(1)![]() ;(2)50 km/h;(3)90 km/h.
;(2)50 km/h;(3)90 km/h.
【解析】
(1)设K=mv2+nsv,则P=mv2+nsv+1000,利用待定系数法求解可得;
(2)将P=500代入(1)中解析式,解方程可得;
(3)将s=180代入解析式后,配方成顶点式可得最值情况.
解:(1)设K=mv2+nsv,则P=mv2+nsv+1000,
由题意得: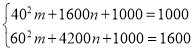 ,
,
整理得:![]() ,
,
解得:![]() ,
,
则P=﹣v2+sv+1000;
(2)根据题意得﹣v2+40v+1000=500,
整理得:v2﹣40v﹣500=0,
解得:v=﹣10(舍)或v=50,
答:平均速度为50km/h;
(3)当s=180时,P=﹣v2+180v+1000=﹣(v﹣90)2+9100,
∴当v=90时,P最大=9100,
答:若行驶指数值最大,平均速度的值为90km/h.


科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小蓉从格致楼底楼点A处沿立人大礼堂旁的台阶AB拾阶而上,步行20米后到达万象楼楼底点B,再从点B直线行进15米到达直通博雅楼的台阶底端C,然后沿台阶CD步行至博雅楼底楼的小平台D.在D点处测得竖立于百汇园旁的万象楼BE的楼顶点E的仰角为30°.如图所示,已知台阶AB与水平地面夹角为45°,台阶CD与水平地面夹角为60°,CD=12米,点A,B,C,D,E在同一平面.则格致楼楼底点A到万象楼楼顶点E的垂直高度约为( )(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
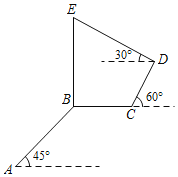
A.22.1米B.35.2米C.27.3米D.36.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
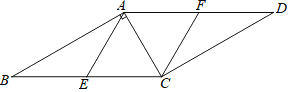
【题目】如图,已知点E,F分别是平行四边形ABCD的边BC,AD上的中点.
(1)AE与CF的关系是 ,请证明;
(2)若∠BAC= °时,四边形AECF是菱形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
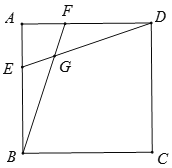
【题目】如图,在正方形ABCD中,AB=a,E、F分别是AB、AD边上的点,BF,DE相交于点G,若AE=![]() AB,AF=
AB,AF=![]() AD,则四边形BCDG的面积是( )
AD,则四边形BCDG的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x+5经过点A,C.
(1)求抛物线的解析式;
(2)如图(2),若过点B的直线交直线AC于点M.
①当BM⊥AC时,过抛物线上一动点P(不与点B,C重合),作直线BM的平行线交AC于点Q,若以点B,M,Q,P为顶点的四边形是平行四边形,求点P的横坐标;
②连结BC,当直线BM与直线AC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com