
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌХзЮяЯпyЃНax2+6x+cНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯпyЃНx+5ОЙ§ЕуAЃЌCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌШєЙ§ЕуBЕФжБЯпНЛжБЯпACгкЕуMЃЎ
ЂйЕБBMЁЭACЪБЃЌЙ§ХзЮяЯпЩЯвЛЖЏЕуPЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЌзїжБЯпBMЕФЦНааЯпНЛACгкЕуQЃЌШєвдЕуBЃЌMЃЌQЃЌPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓЕуPЕФКсзјБъЃЛ
ЂкСЌНсBCЃЌЕБжБЯпBMгыжБЯпACЕФМаНЧЕШгкЁЯACBЕФ2БЖЪБЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНx2+6x+5ЃЛЃЈ2ЃЉЂйЕуPЕФКсзјБъЮЊЉ4ЃЌ![]() Лђ
Лђ![]() ЃЛЂкЕуMЕФзјБъЮЊЃЈ
ЃЛЂкЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуAЃЌCЕФзјБъЃЌгЩЕуAЃЌCЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуBЕФзјБъЃЛ
ЂйЗжЫФБпаЮBMQPЮЊЦНааЫФБпаЮКЭЫФБпаЮBMPQЮЊЦНааЫФБпаЮСНжжЧщПіПМТЧЃКЃЈiЃЉЕБЫФБпаЮBMQPЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуBзїBP1ЁЮACЃЌНЛХзЮяЯпгкЕуP1ЃЌгЩжБЯпACЕФНтЮіЪННсКЯЕуBЕФзјБъПЩЕУГіжБЯпBP1ЕФНтЮіЪНЃЌСЊСЂжБЯпBP1КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЕУГіЕуP1ЕФКсзјБъЃЛЃЈiiЃЉЕБЫФБпаЮBMPQЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуAзїADЁЮyжсЃЌНЛжБЯпBMгкЕуDЃЌвзЧѓЕуDЕФзјБъЮЊЃЈЉ5ЃЌ4ЃЉЃЌЙ§ЕуDзїжБЯпP2P3ЁЮACЃЌНЛХзЮяЯпгкЕуP2ЃЌP3ЃЌгЩжБЯпACЕФНтЮіЪННсКЯЕуDЕФзјБъПЩЕУГіжБЯпP2P3ЕФНтЮіЪНЃЌСЊСЂжБЯпP2P3КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуP2ЃЌP3ЕФКсзјБъЃЛ
ЂкзїBCЕФДЙжБЦНЗжЯпlЃЌДЙзуЮЊEЃЌНЛACгкЕуM1ЃЌзїBNЁЭACгкЕуNЃЌзїЕуM1ЙигкЕуNЕФЖдГЦЕуM2ЃЌM1ЃЌM2ЗћКЯЬѕМўЃЌгЩЕуBЃЌCЕФзјБъПЩЧѓГіжБЯпBCЕФНтЮіЪНМАЕуEЕФзјБъЃЌНсКЯжБЯпlЁЭBCПЩЧѓГіжБЯпlЕФНтЮіЪНЃЌСЊСЂжБЯпlКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуM1ЕФзјБъЃЛгЩжБЯпACЕФНтЮіЪНЁЂЕуBЕФзјБъМАBNЁЭACПЩЧѓГіжБЯпONЕФНтЮіЪНЃЌСЊСЂжБЯпONКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуNЕФзјБъЃЌдйНсКЯЕуNЮЊЯпЖЮM1M2ЕФжаЕуПЩЧѓГіЕуM2ЕФзјБъЃЎ
ЃЈ1ЃЉЕБxЃН0ЪБЃЌyЃНx+5ЃН5ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЃЛ
ЕБyЃН0ЪБЃЌx+5ЃН0ЃЌ
НтЕУЃКxЃНЉ5ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈЉ5ЃЌ0ЃЉЃЎ
НЋAЃЈЉ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ5ЃЉДњШыyЃНax2+6x+cЃЌЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2+6x+5ЃЎ
ЃЈ2ЃЉЕБyЃН0ЪБЃЌx2+6x+5ЃН0ЃЌ
НтЕУЃКx1ЃНЉ5ЃЌx2ЃНЉ1ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЎ
ЂйЁпPQЁЮBMЃЌ
ЁрЗжСНжжЧщПіПМТЧЃЌШчЭМ1ЫљЪОЃК
ЃЈiЃЉЕБЫФБпаЮBMQPЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуBзїBP1ЁЮACЃЌНЛХзЮяЯпгкЕуP1ЃЎ
ЁпжБЯпACЕФНтЮіЪНЮЊyЃНx+5ЃЌ
ЁрЩшжБЯпBP1ЕФНтЮіЪНЮЊyЃНx+bЃЌ
НЋBЃЈЉ1ЃЌ0ЃЉДњШыyЃНx+bЃЌЕУЃКЉ1+bЃН0ЃЌ
НтЕУЃКbЃН1ЃЌ
ЁржБЯпBP1ЕФНтЮіЪНЮЊyЃНx+1ЃЎ
СЊСЂжБЯпBP1КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК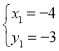 ЃЌ
ЃЌ ЃЌ
ЃЌ
ЁрЕуP1ЕФКсзјБъЮЊЉ4ЃЛ
ЃЈiiЃЉЕБЫФБпаЮBMPQЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуAзїADЁЮyжсЃЌНЛжБЯпBMгкЕуDЃЌЙ§ЕуDзїжБЯпP2P3ЁЮACЃЌНЛХзЮяЯпгкЕуP2ЃЌP3ЃЎ
ЁпOAЃНOCЃЌ
ЁрЁЯOACЃН45ЁуЃЎ
ЁпBMЁЭACЃЌDAЁЭABЃЌ
ЁрЁЯAMBЃН90ЁуЃЌЁЯABMЃН45ЁуЃЌЁЯADMЃН45ЁуЃЎ
дкЁїAMDКЭЁїAMBжаЃЌ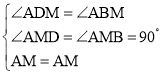 ЃЌ
ЃЌ
ЁрЁїAMDЁеЁїAMBЃЈAASЃЉЃЌ
ЁрADЃНABЃЌDMЃНBMЃЎ
ЁрЕуDЕФзјБъЮЊЃЈЉ5ЃЌ4ЃЉЃЎ
гжЁпжБЯпACЕФНтЮіЪНЮЊyЃНx+5ЃЌ
ЁржБЯпP2P3ЕФНтЮіЪНЮЊyЃНx+9ЃЎ
СЊСЂжБЯпP2P3КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК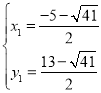 ЃЌ
ЃЌ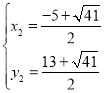 ЃЌ
ЃЌ
ЁрЕуP2ЕФКсзјБъЮЊ![]() ЃЌЕуP3ЕФКсзјБъЮЊ
ЃЌЕуP3ЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕуPЕФКсзјБъЮЊЉ4ЃЌ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉзїBCЕФДЙжБЦНЗжЯпlЃЌДЙзуЮЊEЃЌНЛACгкЕуM1ЃЌзїBNЁЭACгкЕуNЃЌзїЕуM1ЙигкЕуNЕФЖдГЦЕуM2ЃЌM1ЃЌM2ЗћКЯЬѕМўЃЎШчЭМ2ЫљЪОЃЎ
ЁпЕуBЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЃЌ
ЁрЕуEЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌжБЯпBCЕФНтЮіЪНЮЊyЃН5x+5ЃЌ
ЃЉЃЌжБЯпBCЕФНтЮіЪНЮЊyЃН5x+5ЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊyЃНЉ![]() x+
x+![]() ЃЎ
ЃЎ
СЊСЂжБЯпlКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК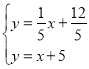 ЃЌ
ЃЌ
НтЕУЃК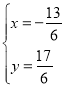 ЃЌ
ЃЌ
ЁрЕуM1ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпжБЯпACЕФНтЮіЪНЮЊyЃНx+5ЃЌЕуBЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌBNЁЭACЃЌ
ЁржБЯпONЕФНтЮіЪНЮЊyЃНЉxЉ1ЃЎ
СЊСЂжБЯпONКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуNЕФзјБъЮЊЃЈЉ3ЃЌ2ЃЉЃЎ
гжЁпЕуNЮЊЯпЖЮM1M2ЕФжаЕуЃЌ
ЁрЕуM2ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁрЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊдЄЗРДЋШОВЁЃЌФГаЃЖЈЦкЖдНЬЪвНјааЁАвЉбЌЯћЖОЁБЃЎвбжЊвЉЮяШМЩеНзЖЮЃЌЪвФкУПСЂЗНУзПеЦјжаЕФКЌвЉСП ![]() гывЉЮядкПеЦјжаЕФГжајЪБМф
гывЉЮядкПеЦјжаЕФГжајЪБМф![]() ГЩе§БШР§ЃЛШМЩеКѓЃЌ
ГЩе§БШР§ЃЛШМЩеКѓЃЌ![]() гы
гы![]() ГЩЗДБШР§ЃЈШчЭМЫљЪОЃЉЃЎЯжВтЕУвЉЮя
ГЩЗДБШР§ЃЈШчЭМЫљЪОЃЉЃЎЯжВтЕУвЉЮя![]() ЗжжгШМЭъЃЌДЫЪБНЬЪвФкУПСЂЗНУзПеЦјКЌвЉСПЮЊ
ЗжжгШМЭъЃЌДЫЪБНЬЪвФкУПСЂЗНУзПеЦјКЌвЉСПЮЊ![]() ЃЎИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЎИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЗжБ№ЧѓГівЉЮяШМЩеЪБМАШМЩеКѓ ![]() Йигк
Йигк![]() ЕФКЏЪ§БэДяЪНЃЎ
ЕФКЏЪ§БэДяЪНЃЎ
ЃЈ2ЃЉЕБУПСЂЗНУзПеЦјжаЕФКЌвЉСПЕЭгк![]() ЪБЃЌЖдШЫЬхЗНФмЮоЖОКІзїгУЃЌФЧУДДгЯћЖОПЊЪМЃЌдкФФИіЪБЖЮЯћЖОШЫдБВЛФмЭЃСєдкНЬЪвРяЃП
ЪБЃЌЖдШЫЬхЗНФмЮоЖОКІзїгУЃЌФЧУДДгЯћЖОПЊЪМЃЌдкФФИіЪБЖЮЯћЖОШЫдБВЛФмЭЃСєдкНЬЪвРяЃП
ЃЈ3ЃЉЕБЪвФкПеЦјжаЕФКЌвЉСПУПСЂЗНУзВЛЕЭгк![]() ЕФГжајЪБМфГЌЙ§
ЕФГжајЪБМфГЌЙ§![]() ЗжжгЃЌВХФмгааЇЩБУ№ФГжжДЋШОВЁЖОЃЎЪдХаЖЯДЫДЮЯћЖОЪЧЗёгааЇЃЌВЂЫЕУїРэгЩЃЎ
ЗжжгЃЌВХФмгааЇЩБУ№ФГжжДЋШОВЁЖОЃЎЪдХаЖЯДЫДЮЯћЖОЪЧЗёгааЇЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЕФФкНгЁїABCЕФЭтНЧЁЯACEЕФЦНЗжЯпНЛЁбOгкЕуDЃЎDFЁЭACЃЌДЙзуЮЊFЃЌDEЁЭBCЃЌДЙзуЮЊEЃЎИјГіЯТСа4ИіНсТлЃКЂйCEЃНCFЃЛЂкЁЯACBЃНЁЯEDFЃЛЂлDEЪЧЁбOЕФЧаЯпЃЛЂм![]() ЃЎЦфжавЛЖЈГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ
ЃЎЦфжавЛЖЈГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ
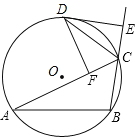
A.ЂйЂкЂлB.ЂкЂлЂмC.ЂйЂлЂмD.ЂйЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊВтСПФГЬижжГЕСОЕФадФмЃЌбаОПжЦЖЈСЫааЪЛжИЪ§![]() ЃЌЖј
ЃЌЖј![]() ЕФДѓаЁгыЦНОљЫйЖШ
ЕФДѓаЁгыЦНОљЫйЖШ![]() КЭааЪЛТЗГЬ
КЭааЪЛТЗГЬ![]() гаЙи(ВЛПМТЧЦфЫћвђЫи)ЃЌ
гаЙи(ВЛПМТЧЦфЫћвђЫи)ЃЌ![]() гЩСНВПЗжЕФКЭзщГЩЃЌвЛВПЗжгы
гЩСНВПЗжЕФКЭзщГЩЃЌвЛВПЗжгы![]() ГЩе§БШЃЌСэвЛВПЗжгы
ГЩе§БШЃЌСэвЛВПЗжгы![]() ГЩе§БШЃЎдкЪЕбщжаЕУЕНСЫБэИёжаЕФЪ§Он:
ГЩе§БШЃЎдкЪЕбщжаЕУЕНСЫБэИёжаЕФЪ§Он:
ЫйЖШ |
|
|
ТЗГЬ |
|
|
жИЪ§ |
|
|
ЃЈ1ЃЉгУКЌ![]() КЭ
КЭ![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО![]() ;
;
ЃЈ2ЃЉЕБааЪЛжИЪ§ЮЊ![]() ЃЌЖјааЪЛТЗГЬЮЊ
ЃЌЖјааЪЛТЗГЬЮЊ![]() ЪБЃЌЧѓЦНОљЫйЖШЕФжЕ;
ЪБЃЌЧѓЦНОљЫйЖШЕФжЕ;
ЃЈ3ЃЉЕБааЪЛТЗГЬЮЊ![]() ЪБЃЌШєааЪЛжИЪ§жЕзюДѓЃЌЧѓЦНОљЫйЖШЕФжЕЃЎ
ЪБЃЌШєааЪЛжИЪ§жЕзюДѓЃЌЧѓЦНОљЫйЖШЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПеХРЯЪІЮЊСЫНтбЇЩњПЮЧАдЄЯАЕФЧщПіЃЌЖдВПЗжбЇЩњНјааСЫИњзйЕїВщЃЌВЂНЋЕїВщНсЙћЗжЮЊЫФРрЃЌAЃККмКУЃЛBЃКНЯКУЃЛCЃКвЛАуЃЛDЃКНЯВюЃЎжЦГЩвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉеХРЯЪІвЛЙВЕїВщСЫЁЁ ЁЁУћЭЌбЇЃП
ЃЈ2ЃЉCРрХЎЩњгаЁЁ ЁЁУћЃЌDРрФаЩњгаЁЁ ЁЁУћЃЛ
ЃЈ3ЃЉЮЊСЫЙВЭЌНјВНЃЌеХРЯЪІЯыДгБЛЕїВщЕФAРрКЭDРрбЇЩњжаИїЫцЛњбЁШЁвЛЮЛЭЌбЇНјааЁАвЛАявЛЁБЛЅжњбЇЯАЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЧѓГіЫљбЁСНЮЛЭЌбЇЧЁКУЖМЪЧФаЭЌбЇЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕквЛЁЂШ§ЯѓЯоФкЕФ
ЕФЭМЯѓЯрНЛгкЕквЛЁЂШ§ЯѓЯоФкЕФ![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБНгаДГіЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдк![]() жсЩЯеввЛЕу
жсЩЯеввЛЕу![]() ЪЙ
ЪЙ![]() зюДѓЃЌЧѓ
зюДѓЃЌЧѓ![]() ЕФзюДѓжЕМАЕу
ЕФзюДѓжЕМАЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁїDCEЪЧЁїABCШЦзХЕуCЫГЪБеыЗНЯђа§зЊЕУЕНЕФЃЌДЫЪБBЁЂCЁЂEдкЭЌвЛжБЯпЩЯЃЎ
ЃЈ1ЃЉа§зЊНЧЕФДѓаЁЃЛ
ЃЈ2ЃЉШєAB=10ЃЌAC=8ЃЌЧѓBEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЄЮЊ![]() ЕФДКгЮЖгЮщЃЌвд
ЕФДКгЮЖгЮщЃЌвд![]() ЕФЫйЖШЯђЖЋааНјЃЌШчЭМ1КЭЭМ2ЃЌЕБЖгЮщХХЮВааНјЕНЮЛжУ
ЕФЫйЖШЯђЖЋааНјЃЌШчЭМ1КЭЭМ2ЃЌЕБЖгЮщХХЮВааНјЕНЮЛжУ![]() ЪБЃЌдкХХЮВДІЕФМзгавЛЮяЦЗвЊЫЭЕНХХЭЗЃЌЫЭЕНКѓСЂМДЗЕЛиХХЮВЃЌМзЕФЭљЗЕЫйЖШОљЮЊ
ЪБЃЌдкХХЮВДІЕФМзгавЛЮяЦЗвЊЫЭЕНХХЭЗЃЌЫЭЕНКѓСЂМДЗЕЛиХХЮВЃЌМзЕФЭљЗЕЫйЖШОљЮЊ![]() ЃЌЕБМзЗЕЛиХХЮВКѓЃЌЫћМАЖгЮщОљЭЃжЙааНјЃЎЩшХХЮВДгЮЛжУ
ЃЌЕБМзЗЕЛиХХЮВКѓЃЌЫћМАЖгЮщОљЭЃжЙааНјЃЎЩшХХЮВДгЮЛжУ![]() ПЊЪМааНјЕФЪБМфЮЊ
ПЊЪМааНјЕФЪБМфЮЊ![]() ЃЌХХЭЗгы
ЃЌХХЭЗгы![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]()
ЃЈ1ЃЉЕБ![]() ЪБЃЌНтД№ЃК
ЪБЃЌНтД№ЃК
ЂйЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЈВЛаД
ЕФКЏЪ§ЙиЯЕЪНЃЈВЛаД![]() ЕФШЁжЕЗЖЮЇЃЉЃЛ
ЕФШЁжЕЗЖЮЇЃЉЃЛ
ЂкЕБМзИЯЕНХХЭЗЮЛжУЪБЃЌЧѓ![]() ЕФжЕЃЛдкМзДгХХЭЗЗЕЛиЕНХХЮВЙ§ГЬжаЃЌЩшМзгыЮЛжУ
ЕФжЕЃЛдкМзДгХХЭЗЗЕЛиЕНХХЮВЙ§ГЬжаЃЌЩшМзгыЮЛжУ![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЈВЛаД
ЕФКЏЪ§ЙиЯЕЪНЃЈВЛаД![]() ЕФШЁжЕЗЖЮЇЃЉ
ЕФШЁжЕЗЖЮЇЃЉ
ЃЈ2ЃЉЩшМзетДЮЭљЗЕЖгЮщЕФзмЪБМфЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЈВЛаД
ЕФКЏЪ§ЙиЯЕЪНЃЈВЛаД![]() ЕФШЁжЕЗЖЮЇЃЉЃЌВЂаДГіЖгЮщдкДЫЙ§ГЬжаааНјЕФТЗГЬЃЎ
ЕФШЁжЕЗЖЮЇЃЉЃЌВЂаДГіЖгЮщдкДЫЙ§ГЬжаааНјЕФТЗГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЖдГЦжсЪЧжБЯп
ЕФЭМЯѓШчЭМЫљЪОЃЌЖдГЦжсЪЧжБЯп![]() ЃЎЯТСаНсТлЃКЂй
ЃЎЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() (
(![]() ЮЊЪЕЪ§)ЃЎЦфжаНсТле§ШЗЕФИіЪ§ЮЊ( )
ЮЊЪЕЪ§)ЃЎЦфжаНсТле§ШЗЕФИіЪ§ЮЊ( )
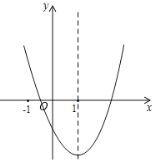
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com